Actual visible points Batch Compilation commands

$N$ 차원 좌표계에는 여러 개의 점들이 있다. 이들은 $M$ 개의 자연수 $X_{1}, ..., X_{M}$를 이용해 나타낼 수 있는데, 각 $X_{i}$가 나타내는 점들의 집합 $S_{i}$는 아래와 같다.

Si =  {(x1, x2, ..., xN) | 1 ≤ x1 ≤ x2 ≤ ... ≤ xn = Xi, 각 x는 모두 자연수}

이제 모든 $S_{i}$ ($1 \le i \le M$)을 모아 이 점들의 집합을 $S$라고 하자. 즉 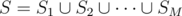이다. $S$에 속한 점들 중에서 $N$차원 좌표계의 원점 $(0, 0, ..., 0)$에서 보이는 점들의 개수를 구하고 싶다. 어떤 점이 보인다는 것은 원점에서 그 점까지 이은 선분 위에 원점과 그 점을 제외한 다른 점이 없다는 것이다.

입력 형식

첫 번째 줄에는 두 개의 자연수 $N$, $M$ ($1 \le ?M \le 100, 000$)이 공백으로 구분되어 주어진다.

다음부터 $M$ 개의 줄의 $i$번째 줄에는 하나의 자연수 $X_{i}$ ($1 \le X_{i} \le 100, 000$)가 주어진다. 각 $X_{i}$들 중에 중복되는 수는 없다.

쉬운 문제에서는 $N = 2$을 만족하는 입력이 주어진다.

어려운 문제에서는 $2 \le N \le 100,000$을 만족하는 입력이 주어진다.

출력 형식

주어진 점들 중에서 원점에서 보이는 점들의 개수를 $1,000,000,007$로 나눈 나머지를 출력한다.

예제

입력

2 4
1
2
3
4

출력

6

좌표계에 있는 점들은 $(1, 1), (1, 2), (2, 2), (1, 3), (2, 3), (3, 3), (1, 4), (2, 4), (3, 4), (4, 4)$이다.

보이는 점은 $(1, 1), (1, 2), (1, 3), (2, 3), (1, 4), (3, 4)$로 총 6개이다.