가장 안전한 경로 Batch 컴파일 명령
| 시간 제한 | 메모리 제한 | 제출 횟수 | 통과한 사람 수 | 비율 |
|---|---|---|---|---|
| 600 ms | 128 MiB | 6 | 2 | 33.33% |
- 참고 원래 시간 제한은 0.2초입니다. 공식 답안이 0.2초 안에 나오지 않아 시간 제한을 늘였습니다.
승현이는 여행하기를 좋아해서, 프로그래머들에게 임의의 한 도시에서 출발하여 또다른 도시에 도착하는 최단 경로를 찾는 것을 도와 달라고 요청하고는 합니다. 몇 년 간의 여행 후, 그는 최단 경로가 언제나 가장 시간이 절약되는 경로는 아니라는 것을 깨닫게 되었습니다. 이러한 현상은 최단 경로 상의 도로들이 매우 상태가 좋지 않아서 다시 돌아가서 또다른 경로를 찾아야 할 때 발생할 수 있습니다. 그래서 이번에는 그는 가장 안전한 경로를 찾는 데에 관심이 있습니다.
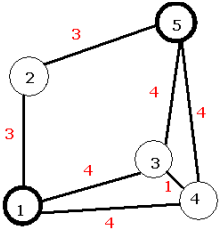
$V$개의 도시와 $E$개의 도로가 있습니다. 도시들에는 $1$ 이상 $V$ 이하의 번호가 붙어 있습니다. 각 도로는 서로 다른 두 개의 도시를 연결하며 양방향입니다. 예를 들어, 아래 그림을 봅시다.
각 원은 도시를 나타내고 그 안에 있는 숫자는 도시 번호를 나타냅니다. 각 선분은 도로를 나타내며 그 옆의 숫자는 길이를 나타냅니다.
승현이가 1번 도시에서 출발하여 5번 도시에 도착하고자 한다면, 최단 경로는 2번 도시를 방문한 뒤 5번 도시에 도착하는 것이 됩니다. 이 경로는 <1, 2, 5>와 같이 쓸 수 있습니다. 하지만, 승현이는 이상적이지 않은 상황에서의 최단 경로를 알고자 합니다. 예를 들어, 1번 도시와 2번 도시를 잇는 도로가 파괴되었다면, 최단 경로는 <1, 3, 5>가 될 것이고 그 길이는 8입니다. 만약 1번 도시와 2번 도시를 잇는 도로는 멀쩡하지만 2번 도시와 5번 도시를 잇는 도로가 파괴되었다면, 승현이는 2번 도시에서 다시 1번 도시로 돌아간 뒤 3번 도시를 거쳐 5번 도시에 도착해야만 합니다. 이 시나리오에서 승현이가 이동한 거리는 $3 + 3 + 8 = 14$입니다.
$X_{1}$번 도시에서 $X_{N}$번 도시까지 <$X_{1}$, $X_{2}$, $X_{3}$, ..., $X_{N}$>의 경로로 이동하고자 한다면, 승현이는 이 경로에 대해 "비이상적 길이"라는 것을 아래와 같이 정의합니다.
max {
모든 도로가 멀쩡하다고 가정할 때 distance(X1, X2, X3, ..., XN),
X1와 X2를 잇는 도로가 파괴되었다고 가정했을 때 X1과 X2 사이의 최단 경로의 길이,
distance(X1, X2) + X2와 X3를 잇는 도로가 파괴되었다고 가정했을 때 X2과 XN 사이의 최단 경로의 길이,
distance(X1, X2, X3) + X3와 X4를 잇는 도로가 파괴되었다고 가정했을 때 X3과 XN 사이의 최단 경로의 길이,
...,
distance(X1, X2, X3, ..., XN-2) + XN-2와 XN-1를 잇는 도로가 파괴되었다고 가정했을 때 XN-2과 XN 사이의 최단 경로의 길이,
distance(X1, X2, X3, ..., XN-1) + XN-1와 XN를 잇는 도로가 파괴되었다고 가정했을 때 XN-1과 XN 사이의 최단 경로의 길이
}
이 때 distance($X_{1}$, $X_{2}$, ..., $X_{p}$)는 ($X_{1}$과 $X_{2}$를 잇는 도로의 길이 + $X_{2}$과 $X_{3}$를 잇는 도로의 길이 + ... + $X_{p-1}$과 $X_{p}$를 잇는 도로의 길이)를 나타냅니다.
위의 정의에 따르면 경로 <1, 2, 5>의 비이상적 길이는 $\max(6, 8, 14) = 14$입니다. 이것보다 더 나은 경로가 있는데, 바로 <1, 3, 5>입니다. 파괴된 도로가 없다면 최단 경로는 8입니다. 1번 도시와 3번 도시를 잇는 도로가 파괴되었다면, 경로의 길이는 6입니다. (<1, 2, 5>) 만약 3번 도시와 5번 도시를 잇는 도로가 파괴되었다면 (1번 도시에서부터 3번 도시에 도착한 후에), 승현이는 4번 도시를 거쳐 5번 도시를 방문하면 되며 이 때 경로의 길이는 9입니다. 따라서 <1, 3, 5>의 비이상적 길이는 $\max(8, 6, 9) = 9$가 됩니다.
마침내, 승현이는 "가장 안전한 경로"를 비이상적 길이가 가장 짧은 경로로, "가장 안전한 경로의 길이"를 가장 안전한 경로의 길이로 정의합니다. 따라서, 위의 예제에서 가장 안전한 경로는 <1, 3, 5>이며 그 길이는 9가 됩니다.
도시들과 도로들의 정보가 주어질 때, $S$번 도시에서 출발하여 $T$번 도시에 도착하는 가장 안전한 경로의 길이를 찾는 프로그램을 작성하세요.
입력 형식
첫 번째 줄에 네 개의 정수 $V$, $E$, $S$, $T$가 주어집니다. 다음 $E$개 줄에는 3개의 정수 $a$, $b$, $c$가 주어지는데, $a$번 도시와 $b$번 도시를 잇는 길이가 $c$인 양방향 도로가 존재한다는 것입니다.
출력 형식
가장 안전한 경로의 길이를 출력합니다.
예제
| 입력 | 출력 |
|---|---|
| 5 7 1 5 1 2 3 2 5 3 1 3 4 3 5 4 1 4 4 4 5 4 4 3 1 |
9 |
| 4 5 1 4 1 2 1 2 3 1 3 4 1 1 3 2 2 4 2 |
3 |
예제 설명
첫 번째 예제는 위에서 기술되어 있습니다.
두 번째 예제에서 가장 안전한 경로는 <1, 2, 4>이며 그 길이는 $\max(3, 3, 3) = 3$입니다. 참고로 경로 <1, 3, 4>의 비이상적 길이는 5이고, <1, 2, 3, 4>의 비이상적 길이는 5입니다.
서브태스크
각 서브태스크에서,
- $1 \le S, T \le V$
- $S \neq T$
- $1 \le E \le V \times (V-1) / 2$
- $1 \le a, b \le V$
- $1 \le c \le 10,000$
- 각 도로는 서로 다른 두 도시를 연결합니다.
- 모든 서로 다른 두 도시의 쌍에 대해 이 도시들 사이에는 최대 1개의 도로가 존재합니다.
- 어떤 도로가 파괴되었다면, $S$에서 출발하여 $T$에 도착하는 대안 경로가 적어도 하나 존재한다는 것이 보장됩니다.
서브태스크 1 (14점)
- $1 \le V \le 6$
서브태스크 2 (30점)
- $1 \le V \le 100$
서브태스크 3 (25점)
- $1 \le V \le 250$
서브태스크 4 (18점)
- $1 \le V \le 500$
서브태스크 5 (13점)
- $1 \le V \le 2,500$
- 처음에 $S$에서 출발하여 $T$에 도착하는 단순 경로가 정확히 두 개 존재합니다.