Pinball Batch 컴파일 명령

상수는 Pinball이라는 게임을 좋아합니다. Pinball의 규칙은 다음과 같습니다.

Pinball의 놀이판은 $(M+2)$행 $N$열의 정사각형 격자들로 구성된 격자판입니다. 놀이판의 첫 번째 줄은 판의 꼭대기이고, $(M+2)$번째 줄은 바닥입니다. $i$번째 행의 $j$번째 열에 있는 정사각형 격자는 $(i, j)$로 표현됩니다.

공은 놀이판의 첫 번째 줄에 있는 격자들 중 하나에 나타나서, 바닥을 향해 수직으로 떨어집니다. 다시 말해, 만약 어떤 공이 $(1, i)$ ($1 \le i \le N$)에 나타났다면, 이는 $(j, i)$ ($2 \le j \le M+1$)을 통과하여, 바닥의 $(M+2, i)$ 격자에 도착할 것입니다. 상수는 공을 성공적으로 되받아 친다면 점수를 얻게 됩니다.

어느 날, 상수는 공을 되받아치기 어렵다는 것을 눈치챘는데, 공이 바닥의 어떤 격자에나 등장할 수 있기 때문입니다. 상수는 아래에 설명된 장치들을 놀이판 위에 적절하게 설치하여 공이 도달할 수 있는 바닥의 격자가 단 하나 있도록 하려고 합니다.

$1$ 이상 $M$ 이하의 번호가 붙은 $M$개의 장치들이 있습니다. 각 장치는 놀이판의 행들과 평행합니다. $I$ ($1 \le i \le M$)번째 장치는 $(i+1, A_{i})$부터 $(i+1, B_{i})$까지의 격자들에 위치해 있습니다. 따라서 이 장치는 총 $B_{i} - A_{i} + 1$개의 격자들을 덮습니다. 만약 공이 이 장치가 설치되어 있는 격자에 닿는다면, 공은 $(i+1, C_{i})$로 운반될 것입니다. 그 이후, 이동한 공은 $C_{i}$번 열을 따라 수직하게 떨어질 것입니다. 하나의 장치는 공과 한 번 이상 상호 작용하지 않을 것입니다.

상수가 $i$번째 장치를 설치하기 위해서는 $D_{i}$원을 지불해야 합니다. 상수는 $M$개의 장치들 중 일부를 골라서 놀이판에 설치하여, 공이 도달할 수 있는 바닥의 격자가 단 하나 존재하도록 할 것입니다. 상수는 장치들을 효율적으로 설치하여 총 비용을 줄이고자 합니다.

해야 할 일

놀이판의 크기와 장치들의 정보가 주어질 때, 공이 도달할 수 있는 바닥 격자가 단 하나 존재하도록 장치들을 설치하기 위한 최소 비용을 구하는 프로그램을 작성하세요.

입력 형식

표준 입력으로부터 다음 데이터를 입력받으세요:

• 입력의 첫 번째 줄에는 두 개의 정수 $M, N$이 공백을 사이로 두고 주어집니다. 이것은 이 놀이판이 $(M+2)$개의 행과 $N$개의 열을 가지고 있으며 장치의 수는 $M$개임을 의미합니다.
• 다음 $M$개 줄들 중 $i$번째 줄 ($1 \le i \le M$)에는 네 개의 정수 $A_{i}, B_{i}, C_{i}, D_{i}$가 공백을 사이로 두고 주어집니다. 이것은 $i$번째 장치가 $(i+1, A{i})$에서부터 $(i+1, B_{i})$까지의 격자에 설치되어 있다는 것을 의미합니다. $i$번째 장치는 총 $B_{i} - A_{i} + 1$개의 격자를 덮습니다. $i$번째 장치는 자신이 덮고 있는 격자에 도달한 공을 $(i+1, C_{i})$로 운반할 것입니다. $i$번째 장치를 설치하기 위해서 $D_{i}$원의 비용이 발생합니다.

출력 형식

표준 출력의 첫 번째 줄에 공이 도달할 수 있는 바닥 격자가 단 하나 존재하도록 장치들을 설치하기 위한 최소 비용을 출력하세요. 만약 이 조건을 만족하도록 장치를 놓는 것이 불가능하다면, $-1$을 출력하세요.

제약 조건

모든 입력 데이터는 다음 조건을 만족합니다:

• $1 \le M \le 100,000$
• $2 \le N \le 1,000,000,000$
• $1 \le A_{i} \le C_{i} \le B_{i} \le N$ ($1 \le i \le M$)
• $1 \le D_{i} \le 1,000,000,000$ ($1 \le i \le M$)

서브태스크

서브태스크 1 [11점]

다음 조건을 만족합니다.

• $M \le 10$
• $N \le 1,000$

서브태스크 2 [18점]

다음 조건을 만족합니다.

• $M \le 200$

서브태스크 3 [[22점]

다음 조건을 만족합니다.

• $M \le 1,000$

서브태스크 4 [49점]

추가 조건이 없습니다.

예제 입력 및 출력

입력 1	출력 1
5 6 2 4 3 5 1 2 2 8 3 6 5 2 4 6 4 7 2 4 3 10	25

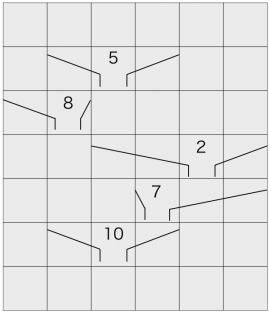
놀이판과 장치들의 위치는 아래 그림과 같습니다. 각 장치 위에 쓰인 수들은 이 장치를 설치하기 위해 필요한 비용을 나타냅니다.

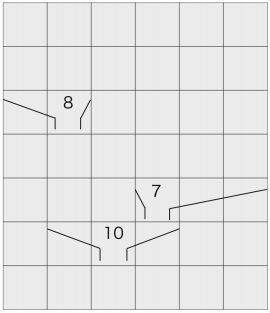
다섯 개의 장치들 중 2번째, 4번째, 5번째 장치를 두면, 놀이판은 아래와 같게 됩니다.

그러면, 꼭대기의 어떤 격자에 공이 등장하더라도 이 공은 바닥의 (7, 3)에 도달할 것입니다. 이들 장치를 설치하는 데에 드는 총 비용은 25원입니다. 여러분은 25를 출력해야 하는데, 25원보다 적은 비용을 들이면서 공이 도달할 수 있는 바닥의 격자가 단 하나 존재하도록 할 수 없기 때문입니다.

입력 2	출력 2
3 5 2 4 3 10 1 3 1 20 2 5 4 30	-1

불가능한 경우입니다.