Tree Batch
| Time limit | Memory limit | # of submissions | # of submitted users | Solved # | Accepted user ratio |
|---|---|---|---|---|---|
| 2000 ms | 2048 MiB | 577 | 96 | 25 | 26.04% |
Consider a tree consisting of $N$ vertices, numbered from $0$ to $N-1$. Vertex $0$ is called the root. Every vertex, except for the root, has a single parent. For every $i$, such that $1 \leq i < N$, the parent of vertex $i$ is vertex $P[i]$, where $P[i] < i$. We also assume $P[0] = -1$.
For any vertex $i$ ($0 \leq i < N$), the subtree of $i$ is the set of the following vertices:
- $i$, and
- any vertex whose parent is $i$, and
- any vertex whose parent's parent is $i$, and
- any vertex whose parent's parent's parent is $i$, and
- etc.
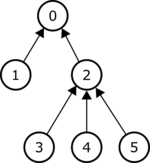
The picture below shows an example tree consisting of $N = 6$ vertices. Each arrow connects a vertex to its parent, except for the root, which has no parent. The subtree of vertex $2$ contains vertices $2, 3, 4$ and $5$. The subtree of vertex $0$ contains all $6$ vertices of the tree and the subtree of vertex $4$ contains only vertex $4$.
Each vertex is assigned a nonnegative integer weight. We denote the weight of vertex $i$ ($0 \leq i < N$) by $W[i]$.
Your task is to write a program that will answer $Q$ queries, each specified by a pair of positive integers $(L, R)$. The answer to the query should be computed as follows.
Consider assigning an integer, called a coefficient, to each vertex of the tree. Such an assignment is described by a sequence $C[0], \ldots, C[N-1]$, where $C[i]$ ($0 \leq i < N$) is the coefficient assigned to vertex $i$. Let us call this sequence a coefficient sequence. Note that the elements of the coefficient sequence can be negative, $0$, or positive.
For a query $(L, R)$, a coefficient sequence is called valid if, for every vertex $i$ ($0 \leq i < N$), the following condition holds: the sum of the coefficients of the vertices in the subtree of vertex $i$ is not less than $L$ and not greater than $R$.
For a given coefficient sequence $C[0], \ldots, C[N-1]$, the cost of a vertex $i$ is $|C[i]| \cdot W[i]$, where $|C[i]|$ denotes the absolute value of $C[i]$. Finally, the total cost is the sum of the costs of all vertices. Your task is to compute, for each query, the minimum total cost that can be attained by some valid coefficient sequence.
It can be shown that for any query, at least one valid coefficient sequence exists.
Implementation Details
You should implement the following two procedures:
void init(std::vector<int> P, std::vector<int> W)
- $P$, $W$: arrays of integers of length $N$ specifying the parents and the weights.
- This procedure is called exactly once in the beginning of the interaction between the grader and your program in each test case.
long long query(int L, int R)
- $L$, $R$: integers describing a query.
- This procedure is called $Q$ times after the invocation of
initin each test case. - This procedure should return the answer to the given query.
Constraints
- $1 \leq N \leq 200,000$
- $1 \leq Q \leq 100,000$
- $P[0] = -1$
- $0 \leq P[i] < i$ for each $i$ such that $1 \leq i < N$
- $0 \leq W[i] \leq 1,000,000$ for each $i$ such that $0 \leq i < N$
- $1 \leq L \leq R \leq 1,000,000$ in each query
Subtasks
| Subtask | Score | Additional Constraints |
|---|---|---|
| 1 | $10$ | $Q \leq 10$; $W[P[i]] \leq W[i]$ for each $i$ such that $1 \leq i < N$ |
| 2 | $13$ | $Q \leq 10$; $N \leq 2,000$ |
| 3 | $18$ | $Q \leq 10$; $N \leq 60,000$ |
| 4 | $7$ | $W[i] = 1$ for each $i$ such that $0 \leq i < N$ |
| 5 | $11$ | $W[i] \leq 1$ for each $i$ such that $0 \leq i < N$ |
| 6 | $22$ | $L = 1$ |
| 7 | $19$ | No additional constraints. |
Examples
Consider the following calls:
init([-1, 0, 0], [1, 1, 1])
The tree consists of $3$ vertices, the root and its $2$ children. All vertices have weight $1$.
query(1, 1)
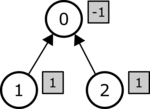
In this query $L = R = 1$, which means the sum of coefficients in every subtree must be equal to $1$. Consider the coefficient sequence $[-1, 1, 1]$. The tree and the corresponding coefficients (in shaded rectangles) are illustrated below.
For every vertex $i$ ($0 \leq i < 3$), the sum of the coefficients of all vertices in the subtree of $i$ is equal to $1$. Hence, this coefficient sequence is valid. The total cost is computed as follows:
| Vertex | Weight | Coefficient | Cost |
|---|---|---|---|
| 0 | 1 | -1 | $\mid -1 \mid \cdot 1 = 1$ |
| 1 | 1 | 1 | $\mid 1 \mid \cdot 1 = 1$ |
| 2 | 1 | 1 | $\mid 1 \mid \cdot 1 = 1$ |
Therefore the total cost is $3$. This is the only valid coefficient sequence, therefore this call should return $3$.
query(1, 2)
The minimum total cost for this query is $2$, and is attained when the coefficient sequence is $[0, 1, 1]$.
Sample Grader
Input format:
N
P[1] P[2] ... P[N-1]
W[0] W[1] ... W[N-2] W[N-1]
Q
L[0] R[0]
L[1] R[1]
...
L[Q-1] R[Q-1]
where $L[j]$ and $R[j]$
(for $0 \leq j < Q$)
are the input arguments in the $j$-th call to query.
Note that the second line of the input contains only $N-1$ integers,
as the sample grader does not read the value of $P[0]$.
Output format:
A[0]
A[1]
...
A[Q-1]
where $A[j]$
(for $0 \leq j < Q$)
is the value returned by the $j$-th call to query.
| File name | Size |
|---|---|
| tree.zip | 2.39 KiB |