트리 Batch
| 시간 제한 | 메모리 제한 | 제출 횟수 | 제출한 사람 수 | 해결한 사람 수 | 정답률 |
|---|---|---|---|---|---|
| 2000 ms | 2048 MiB | 531 | 91 | 25 | 27.47% |
$N$개의 노드로 이루어진 트리를 생각해보자. 각 노드는 $0$부터 $N-1$까지 순서대로 번호가 매겨져 있다. 노드 $0$은 루트이다. 루트를 제외한 모든 노드는 하나의 부모가 있다. $1 \leq i < N$인 모든 $i$에 대해서, 노드 $i$의 부모는 노드 $P[i]$이고, $P[i] < i$이다. $P[0] = -1$이라고 하자.
어떤 노드 $i$ ($0 \leq i < N$)에 대해서, $i$의 서브트리는 다음과 같은 노드들의 집합이다.
- $i$,
- 부모가 $i$인 모든 노드,
- 부모의 부모가 $i$인 모든 노드,
- 부모의 부모의 부모의 노드가 $i$인 모든 노드,
- ...
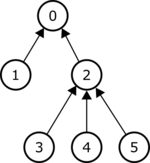
다음 그림은 $N=6$ 개의 노드로 이루어진 트리의 예를 보여주고 있다. 각각의 화살표는 노드를 그 부모와 연결한다. 루트는 부모가 없으므로 예외이다. 노드 $2$의 서브 트리는 노드 ${2, 3, 4, 5}$이다. 노드 $0$의 서브트리는 이 트리의 모든 $6$개의 노드이다. 노드 $4$의 서브트리는 노드 $4$로만 이루어져 있다.
각 노드는 음이 아닌 정수 가중치를 갖고 있다. 노드 $i$ ($0 \leq i < N$)의 가중치를 $W[i]$로 표현하자.
당신이 할 일은 두 양의 정수 $(L, R)$로 이루어진 질의 $Q$ 개를 처리하는 것이다. 질의에 대한 답을 다음과 같이 계산해야 한다.
트리의 각 노드마다 정수값인 계수를 할당해보자. 노드들에 할당된 계수들을 $C[0], \ldots, C[N-1]$로 표현할 수 있다. $C[i]$ ($0 \leq i < N$)는 노드 $i$에 할당된 계수이다. 이 수열을 계수 수열이라고 부르자. 계수 수열은 음수, $0$, 양수를 모두 포함할 수 있음에 유의하자.
질의 $(L, R)$에 대해서 계수 수열이 올바르려면 모든 노드 $i$ ($0 \leq i < N$)에 대해서 다음 조건이 만족되어야 한다: 노드 $i$의 서브트리에 포함된 모든 노드의 계수의 합이, $L$ 이상 $R$ 이하여야 한다.
주어진 계수 수열 $C[0], \ldots, C[N-1]$에서, 노드 $i$의 비용은 $|C[i]| \cdot W[i]$인데, $|C[i]|$는 $C[i]$의 절대값이다. 마지막으로, 전체 비용은 모든 노드의 비용의 합이다. 당신이 할 일은, 각각의 질의에 대해서, 올바른 계수 수열에서 얻을 수 있는 최소 전체 비용을 구하는 것이다.
어떤 질의에 대해서도 최소한 하나의 올바른 계수 수열이 존재한다는 것을 보일 수 있다.
Implementation Details
다음 두 함수를 구현해야 한다.
void init(std::vector<int> P, std::vector<int> W)
- $P$, $W$: 길이 $N$인 배열로 부모와 가중치를 저장한다.
- 이 함수는 각 테스트케이스에서 그레이더와 당신의 프로그램 사이 상호작용이 시작할 때 정확히 한 번 호출된다.
long long query(int L, int R)
- $L$, $R$: 질의를 나타내는 두 정수.
- 이 함수는 각 테스트케이스마다
init이 호출된 다음 $Q$번 호출된다. - 이 함수는 질의에 대한 답을 리턴해야 한다.
Constraints
- $1 \leq N \leq 200,000$
- $1 \leq Q \leq 100,000$
- $P[0] = -1$
- $1 \leq i < N$인 각 $i$에 대해서 $0 \leq P[i] < i$
- $0 \leq i < N$인 각 $i$에 대해서 $0 \leq W[i] \leq 1,000,000$
- 각 질의에 대해 $1 \leq L \leq R \leq 1,000,000$
Subtasks
| Subtask | Score | Additional Constraints |
|---|---|---|
| 1 | $10$ | $Q \leq 10$; $1 \leq i < N$인 각 $i$에 대해서 $W[P[i]] \leq W[i]$ |
| 2 | $13$ | $Q \leq 10$; $N \leq 2,000$ |
| 3 | $18$ | $Q \leq 10$; $N \leq 60,000$ |
| 4 | $7$ | $0 \leq i < N$인 각 $i$에 대해서 $W[i] = 1$ |
| 5 | $11$ | $0 \leq i < N$인 각 $i$에 대해서 $W[i] \leq 1$ |
| 6 | $22$ | $L = 1$ |
| 7 | $19$ | 추가적인 제약 조건이 없다. |
Examples
다음 호출을 생각해보자.
init([-1, 0, 0], [1, 1, 1])
이 트리는 $3$개의 노드로 구성되어 있는데, 루트와 루트의 자식 $2$개이다. 모든 노드는 가중치 $1$이다.
query(1, 1)
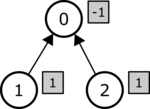
질의 $L = R = 1$이 주어지면, 이 질의는 모든 서브트리의 계수의 합이 $1$이라는 뜻이 된다. 계수 수열이 $[-1, 1, 1]$이라고 생각해보자. 트리와 이에 대응하는 계수가 (색칠한 직사각형) 아래 그림에 있다.
각각의 노드 $i$에 대해서 ($0 \leq i < 3$), $i$의 서브트리의 모든 노드의 계수의 합은 $1$이다. 따라서, 이 계수 수열은 올바르다. 전체 비용은 다음과 같이 계산할 수 있다.
| 노드 | 가중치 | 계수 | 비용 |
|---|---|---|---|
| 0 | 1 | -1 | $\mid -1 \mid \cdot 1 = 1$ |
| 1 | 1 | 1 | $\mid 1 \mid \cdot 1 = 1$ |
| 2 | 1 | 1 | $\mid 1 \mid \cdot 1 = 1$ |
따라서 전체 비용은 $3$이다. 이 계수 수열이 유일한 올바른 계수 수열이므로, 리턴값은 $3$이어야 한다.
query(1, 2)
이 질의에 대한 최소 전체 비용은 $2$인데, 계수 수열이 $[0, 1, 1]$일 때이다.
Sample Grader
입력 형식:
N
P[1] P[2] ... P[N-1]
W[0] W[1] ... W[N-2] W[N-1]
Q
L[0] R[0]
L[1] R[1]
...
L[Q-1] R[Q-1]
$L[j]$와 $R[j]$는 ($0 \leq j < Q$) $j+1$번째로 호출된 query의 파라미터이다.
입력의 두번째 줄에 오직 $N-1$개의 정수만 있다는데 유의하자. 샘플 그레이더는
$P[0]$의 값을 읽지 않기 때문이다.
출력 형식:
A[0]
A[1]
...
A[Q-1]
$A[j]$는 ($0 \leq j < Q$) $j+1$번째로 호출된 query의 리턴값이다.
| 파일명 | 크기 |
|---|---|
| tree.zip | 2.39 KiB |