스핑크스 Interactive
| 시간 제한 | 메모리 제한 | 제출 횟수 | 제출한 사람 수 | 해결한 사람 수 | 정답률 |
|---|---|---|---|---|---|
| 1500 ms | 2048 MiB | 879 | 104 | 35 | 33.65% |
스핑크스는 수수께끼를 냈다. 노드가 $N$개 있는 그래프가 당신에게 주어졌다. 노드는 $0$부터 $N-1$까지 번호가 매겨져 있다. 그래프에는 $M$개의 에지가 있다. 에지는 $0$부터 $M-1$까지 번호가 매겨져 있다. 각 에지는 서로 다른 두 노드를 연결하고 양방향이다. 구체적으로, $0$ 이상 $M-1$이하인 $j$에 대해서, 에지 $j$는 노드 $X[j]$와 $Y[j]$를 연결한다. 주어진 그래프는 두 노드를 어떻게 고르더라도 둘을 연결하는 에지가 최대 하나이다. 두 노드가 하나의 에지로 연결되어 있다면 이 노드는 서로 인접하다고 부른다.
노드의 수열 $v_0, v_1, \ldots, v_k$ ($k \ge 0$)은 $0 \le l < k$ 인 모든 $l$ 에 대해 두 노드 $v_l$와 $v_{l+1}$가 인접하다면 경로라고 불린다. 주어진 그래프는 두 노드를 어떻게 고르더라도 이 둘을 잇는 경로가 있다.
$N+1$가지 종류의 색깔이 있고, 각 색깔은 $0$ 이상 $N$ 이하의 수로 표현된다. 색 $N$은 특별히 스핑크스의 색이라고 부른다. 각 노드마다 하나의 색이 할당되어 있다. 보다 자세하게는, 노드 $i$에 할당된 색은 ($0 \le i \lt N$) $C[i]$이다. 둘 이상의 노드에 같은 색이 할당될 수 있고, 어떤 노드에도 할당되지 않은 색이 있을 수 있다. 스핑크스의 색이 할당된 노드는 없다. 즉, $0 \le C[i] \lt N$ ($0 \le i \lt N$)이다.
경로 $v_0, v_1, \ldots, v_k$ ($k \ge 0$)는 만약 모든 노드가 같은 색이 할당되어 있다면 단색 경로라고 부른다. 즉, $0 \le l \lt k$인 모든 $l$에 대해서 $C[v_l] = C[v_{l+1}]$이다. 추가로, 정점 $p$와 $q$ ($0 \le p \lt N$, $0 \le q \lt N$)가 같은 단색 연결 요소에 속한다는 것은 이 둘이 단색 경로로 연결되어 있다는 뜻이다.
당신은 그래프의 노드와 에지에 대한 정보는 알고 있지만, 노드의 색깔에 대한 정보는 알지 못한다. 다음과 같은 채색 실험을 통해서 노드의 색깔을 알아내려고 한다.
채색 실험에서는 원하는 노드들의 색깔을 바꿀 수 있다. 구체적으로는, 채색 실험을 하기 위해서 먼저 길이 $N$인 배열 $E$를 정해야 한다. $0 \le i \lt N$인 모든 $i$에 대해서 $E[i]$는 $-1$ 이상 $N$ 이하이다. 그 후 각 노드 $i$의 색은 $S[i]$가 되는데, $S[i]$의 값은:
- 만약 $E[i] = -1$이면 $i$의 원래 색인 $C[i]$
- 그렇지 않으면 $E[i]$.
채색 실험을 하는 동안에는 스핑크스의 색을 쓸 수 있다는데 유의하라.
각 노드 $i$의 색을 $S[i]$로 ($0 \le i \lt N$) 다 바꾼 다음에는 스핑크스가 이 그래프에 있는 단색 연결 요소의 수를 알려준다. 새로 칠한 색은 채색 실험을 하는 동안에만 적용되며, 하나의 채색 실험이 끝나면 노드의 색은 원래의 색으로 돌아온다.
당신이 할 일은 최대 $2,750$번 채색 실험을 해서 각 노드의 색을 알아내는 것이다. 모든 인접한 노드의 쌍에 대해서, 이 둘이 같은 색인지 여부를 정확히 맞춘다면 부분 점수를 받을 수 있다.
Implementation Details
다음 함수를 구현해야 한다.
std::vector<int> find_colours(int N,
std::vector<int> X, std::vector<int> Y)
- $N$: 그래프의 노드의 수
- $X$, $Y$: 에지의 정보를 나타내는 길이 $M$인 배열
- 이 함수는 그래프의 노드의 색을 표현하는 길이 $N$인 배열 $G$를 리턴해야 한다.
- 이 함수는 각 테스트케이스마다 정확히 한 번 호출된다.
위 함수는 채색 실험을 하기 위해서 다음 함수를 호출할 수 있다.
int perform_experiment(std::vector<int> E)
- $E$: 어떻게 노드를 칠할 지에 대한 명세가 담긴 길이 $N$인 배열
- 이 함수는 $E$에 저장된 정보에 따라 채색 실험을 한 뒤 그래프에 포함된 단색 연결 요소의 개수를 리턴한다.
- 이 함수는 최대 $2,750$ 번 호출될 수 있다.
그레이더는 적응적(adaptive)이지 않다. 즉, find_colours를 호출하기
전에 노드의 색들은 이미 정해져 있다.
Constraints
- $2 \le N \le 250$
- $N - 1 \le M \le \frac{N \cdot (N - 1)}{2}$
- $0 \le j \lt M$인 각 $j$에 대해 $0 \le X[j] \lt Y[j] \lt N$.
- $0 \le j \lt k \lt M$인 각각의 $j$, $k$에 대해 $X[j] \neq X[k]$이거나 $Y[j] \neq Y[k]$.
- 두 노드를 어떻게 고르더라도 이 둘을 잇는 경로가 있다.
- $0 \le i \lt N$인 각 $i$에 대해 $0 \le C[i] \lt N$.
Subtasks
| Subtask | Score | Additional Constraints |
|---|---|---|
| 1 | $3$ | $N = 2$ |
| 2 | $7$ | $N \le 50$ |
| 3 | $33$ | 주어진 그래프는 경로이다. $M = N - 1$이고 노드 $j$와 $j+1$는 서로 인접한다 ($0 \leq j < M$). |
| 4 | $21$ | 주어진 그래프는 완전 그래프이다. $M = \frac{N \cdot (N - 1)}{2}$ 이고 어떤 두 노드를 고르더라도 이 둘은 서로 인접한다. |
| 5 | $36$ | 추가적인 제약조건이 없다. |
각 서브태스크마다, 여러분의 프로그램이 모든 인접한 노드의 쌍에 대해서, 이 둘이 같은 색인지 여부를 정확히 맞춘다면 부분 점수를 받을 수 있다.
보다 엄밀하게는, 어떤 서브태스크의 모든 테스트케이스에서
find_colours가 리턴한 배열 $G$가 배열 $C$와 동일하면
(즉, $0 \le i \lt N$인 모든 $i$에 대해 $G[i] = C[i]$)
이 서브태스크에 주어진 점수를 모두 받는다.
그렇지 않고, 어떤 서브태스크의 모든 테스트케이스에서
다음을 만족하면 이 서브태스크에 주어진 점수의 $50%$를 받는다.
- $0 \le i \lt N$인 모든 $i$에 대해 $0 \le G[i] \lt N$.
- $0 \le j \lt M$인 모든 $j$에 대해:
- $G[X[j]] = G[Y[j]]$는 $C[X[j]] = C[Y[j]]$일 필요충분조건이다.
Example
다음 호출을 생각해보자.
find_colours(4, [0, 1, 0, 0], [1, 2, 2, 3])
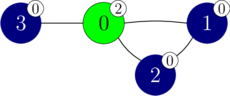
이 예제에서, 우리가 알지 못하지만 이 그래프의 노드들의 색이 $C = [2, 0, 0, 0]$이었다고 가정하자. 이 시나리오는 다음 그림과 같다. 각 노드의 붙어 있는 흰색 레이블은 이 노드의 색이다.
이 함수는 perform_experiment를 다음과 같이 호출할 수 있다.
perform_experiment([-1, -1, -1, -1])
이 호출에서 모든 노드가 원래 색이 유지되므로 색이 달라지는 노드는 없다.
노드 $1$과 노드 $2$를 생각해보자. 이 둘은 모두 색 $0$이고 경로 $1, 2$는 단색 경로이다. 따라서, 노드 $1$과 $2$는 같은 단색 연결 요소에 속한다.
노드 $1$과 노드 $3$을 생각해보자. 이 둘은 모두 색 $0$이지만, 이 둘을 잇는 단색 경로가 없으므로 이 둘은 다른 단색 연결 요소에 속한다.
정리해보면, $3$개의 단색 연결 요소가 있다. 노드 ${0}$, 노드 ${1, 2}$, 노드 ${3}$. 따라서 리턴값은 $3$이다.
이제 이 함수는 perform_experiment를 다음과 같이 호출할 수 있다.
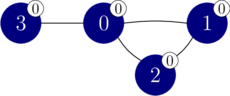
perform_experiment([0, -1, -1, -1])
이 호출에서, 노드 $0$만 색이 $0$으로 바뀌고 그 결과는 다음 그림과 같다.
리턴값은 $1$인데, 모든 노드가 같은 단색 연결 요소에 속하기 때문이다. 따라서 노드 $1$, $2$, $3$은 색 $0$이라고 추론할 수 있다.
이제 이 함수는 perform_experiment를 다음과 같이 호출할 수 있다.
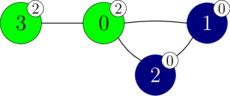
perform_experiment([-1, -1, -1, 2])
이 호출에서, 노드 $3$은 색이 $2$로 바뀌고 그 결과는 다음 그림과 같다.
리턴값은 $2$인데, $2$개의 단색 연결 요소 ${0, 3}$과 ${1, 2}$이 있기 때문이다. 따라서 노드 $0$은 색 $2$라고 추론할 수 있다.
함수 find_colours는 배열 $[2, 0, 0, 0]$을 리턴한다.
$C = [2, 0, 0, 0]$이므로, 만점을 받는다.
만점의 $50%$를 받을 수 있는 리턴값은 여러 가지가 있을 수 있다는데 유의하라. 예를 들면, $[1, 2, 2, 2]$ 또는 $[1, 2, 2, 3]$이다.
Sample Grader
Input format:
N M
C[0] C[1] ... C[N-1]
X[0] Y[0]
X[1] Y[1]
...
X[M-1] Y[M-1]
Output format:
L Q
G[0] G[1] ... G[L-1]
여기에서, $L$은 find_colours가 리턴한 배열 $G$의 길이이며, $Q$는 perform_experiment를 호출한 횟수이다.
| 파일명 | 크기 |
|---|---|
| sphinx.zip | 2.91 KiB |