Sphinx's Riddle Interactive
| Time limit | Memory limit | # of submissions | # of submitted users | Solved # | Accepted user ratio |
|---|---|---|---|---|---|
| 1500 ms | 2048 MiB | 879 | 104 | 35 | 33.65% |
The Great Sphinx has a riddle for you. You are given a graph on $N$ vertices. The vertices are numbered from $0$ to $N - 1$. There are $M$ edges in the graph, numbered from $0$ to $M-1$. Each edge connects a pair of distinct vertices and is bidirectional. Specifically, for each $j$ from $0$ to $M - 1$ (inclusive) edge $j$ connects vertices $X[j]$ and $Y[j]$. There is at most one edge connecting any pair of vertices. Two vertices are called adjacent if they are connected by an edge.
A sequence of vertices $v_0, v_1, \ldots, v_k$ (for $k \ge 0$) is called a path if each two consecutive vertices $v_l$ and $v_{l+1}$ (for each $l$ such that $0 \le l \lt k$) are adjacent. We say that a path $v_0, v_1, \ldots, v_k$ connects vertices $v_0$ and $v_k$. In the graph given to you, each pair of vertices is connected by some path.
There are $N + 1$ colours, numbered from $0$ to $N$. Colour $N$ is special and is called the Sphinx's colour. Each vertex is assigned a colour. Specifically, vertex $i$ ($0 \le i \lt N$) has colour $C[i]$. Multiple vertices may have the same colour, and there might be colours not assigned to any vertex. No vertex has the Sphinx's colour, that is, $0 \le C[i] \lt N$ ($0 \le i \lt N$).
A path $v_0, v_1, \ldots, v_k$ (for $k \ge 0$) is called monochromatic if all of its vertices have the same colour, i.e. $C[v_l] = C[v_{l+1}]$ (for each $l$ such that $0 \le l \lt k$). Additionally, we say that vertices $p$ and $q$ ($0 \le p \lt N$, $0 \le q \lt N$) are in the same monochromatic component if and only if they are connected by a monochromatic path.
You know the vertices and edges, but you do not know which colour each vertex has. You want to find out the colours of the vertices, by performing recolouring experiments.
In a recolouring experiment, you may recolour arbitrarily many vertices. Specifically, to perform a recolouring experiment you first choose an array $E$ of size $N$, where for each $i$ ($0 \le i \lt N$), $E[i]$ is between $-1$ and $N$ inclusive. Then, the colour of each vertex $i$ becomes $S[i]$, where the value of $S[i]$ is:
- $C[i]$, that is, the original colour of $i$, if $E[i] = -1$, or
- $E[i]$, otherwise.
Note that this means that you can use the Sphinx's colour in your recolouring.
Finally, the Great Sphinx announces the number of monochromatic components in the graph, after setting the colour of each vertex $i$ to $S[i]$ ($0 \le i \lt N$). The new colouring is applied only for this particular recolouring experiment, so the colours of all vertices return to the original ones after the experiment finishes.
Your task is to identify the colours of the vertices in the graph by performing at most $2,750$ recolouring experiments. You may also receive a partial score if you correctly determine for every pair of adjacent vertices, whether they have the same colour.
Implementation Details
You should implement the following procedure.
std::vector<int> find_colours(int N,
std::vector<int> X, std::vector<int> Y)
- $N$: the number of vertices in the graph.
- $X$, $Y$: arrays of length $M$ describing the edges.
- This procedure should return an array $G$ of length $N$, representing the colours of vertices in the graph.
- This procedure is called exactly once for each test case.
The above procedure can make calls to the following procedure to perform recolouring experiments:
int perform_experiment(std::vector<int> E)
- $E$: an array of length $N$ specifying how vertices should be recoloured.
- This procedure returns the number of monochromatic components after recolouring the vertices according to $E$.
- This procedure can be called at most $2,750$ times.
The grader is not adaptive, that is,
the colours of the vertices are fixed before a call to find_colours is made.
Constraints
- $2 \le N \le 250$
- $N - 1 \le M \le \frac{N \cdot (N - 1)}{2}$
- $0 \le X[j] \lt Y[j] \lt N$ for each $j$ such that $0 \le j \lt M$.
- $X[j] \neq X[k]$ or $Y[j] \neq Y[k]$ for each $j$ and $k$ such that $0 \le j \lt k \lt M$.
- Each pair of vertices is connected by some path.
- $0 \le C[i] \lt N$ for each $i$ such that $0 \le i \lt N$.
Subtasks
| Subtask | Score | Additional Constraints |
|---|---|---|
| 1 | $3$ | $N = 2$ |
| 2 | $7$ | $N \le 50$ |
| 3 | $33$ | The graph is a path: $M = N - 1$ and vertices $j$ and $j+1$ are adjacent ($0 \leq j < M$). |
| 4 | $21$ | The graph is complete: $M = \frac{N \cdot (N - 1)}{2}$ and any two vertices are adjacent. |
| 5 | $36$ | No additional constraints. |
In each subtask, you can obtain a partial score if your program determines correctly for every pair of adjacent vertices whether they have the same colour.
More precisely,
you get the whole score of a subtask
if in all of its test cases,
the array $G$ returned by find_colours
is exactly the same as array $C$
(i.e. $G[i] = C[i]$
for all $i$ such that $0 \le i \lt N$).
Otherwise,
you get $50%$ of the score for a subtask
if the following conditions hold
in all of its test cases:
- $0 \le G[i] \lt N$ for each $i$ such that $0 \le i \lt N$;
- For each $j$ such that $0 \le j \lt M$:
- $G[X[j]] = G[Y[j]]$ if and only if $C[X[j]] = C[Y[j]]$.
Example
Consider the following call.
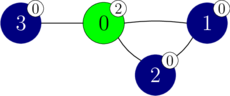
find_colours(4, [0, 1, 0, 0], [1, 2, 2, 3])
For this example, suppose that the (hidden) colours of the vertices are given by $C = [2, 0, 0, 0]$. This scenario is shown in the following figure. Colours are additionally represented by numbers on white labels attached to each vertex.
The procedure may call perform_experiment as follows.
perform_experiment([-1, -1, -1, -1])
In this call, no vertex is recoloured, as all vertices keep their original colours.
Consider vertex $1$ and vertex $2$. They both have colour $0$ and the path $1, 2$ is a monochromatic path. As a result, vertices $1$ and $2$ are in the same monochromatic component.
Consider vertex $1$ and vertex $3$. Even though both of them have colour $0$, they are in different monochromatic components as there is no monochromatic path connecting them.
Overall, there are $3$ monochromatic components, with vertices ${0}$, ${1, 2}$, and ${3}$. Thus, this call returns $3$.
Now the procedure may call perform_experiment as follows.
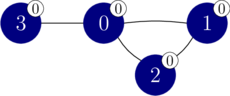
perform_experiment([0, -1, -1, -1])
In this call, only vertex $0$ is recoloured to colour $0$, which results in the colouring shown in the following figure.
This call returns $1$, as all the vertices belong to the same monochromatic component. We can now deduce that vertices $1$, $2$, and $3$ have colour $0$.
The procedure may then call perform_experiment as follows.
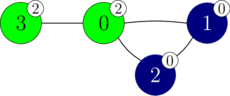
perform_experiment([-1, -1, -1, 2])
In this call, vertex $3$ is recoloured to colour $2$, which results in the colouring shown in the following figure.
This call returns $2$, as there are $2$ monochromatic components, with vertices ${0, 3}$ and ${1, 2}$ respectively. We can deduce that vertex $0$ has colour $2$.
The procedure find_colours then returns the array $[2, 0, 0, 0]$.
Since $C = [2, 0, 0, 0]$, full score is given.
Note that there are also multiple return values, for which $50%$ of the score would be given, for example $[1, 2, 2, 2]$ or $[1, 2, 2, 3]$.
Sample Grader
Input format:
N M
C[0] C[1] ... C[N-1]
X[0] Y[0]
X[1] Y[1]
...
X[M-1] Y[M-1]
Output format:
L Q
G[0] G[1] ... G[L-1]
Here, $L$ is the length of the array $G$ returned by find_colours,
and $Q$ is the number of calls to perform_experiment.
| File name | Size |
|---|---|
| sphinx.zip | 2.91 KiB |