흑백 이미지 찾기 Batch
| 시간 제한 | 메모리 제한 | 제출 횟수 | 제출한 사람 수 | 해결한 사람 수 | 정답률 |
|---|---|---|---|---|---|
| 10000 ms | 512 MiB | 59 | 12 | 4 | 33.33% |
흑백 이미지에는 색이 없다. 따라서 흑백 이미지를 표현할 때에는, 각 픽셀마다 그 픽셀의 밝기를 나타내는 수치 하나만 기록한다. 이 문제에서는 0 이상 65,535 이하의 정수로 한 픽셀의 밝기를 나타낼 수 있다고 하자.
$H \times W$ 크기의 흑백 사진 $I$는 $H \times W$개의 픽셀들이 $H$행 $W$열로 배열된 형태라고 생각하고, $i$ ($1 \le i \le H$)행 $j$ ($1 \le j \le W$)열에 있는 픽셀의 밝기를 $I[i, j]$로 표현하자.
경근이는 $N \times M$ 크기의 흑백 이미지 $A$와 $R \times C$ 크기의 흑백 이미지 $B$를 가지고 있다. 이 때 $N \ge R$, $M \ge C$이다. ($A$가 $B$보다 가로/세로 길이가 모두 더 길다) 경근이는 $A$가 $B$를 표절했다고 생각하고, $A$에서 $B$와 비슷한 부분이 몇 개나 되는지 찾고자 한다.
그 방법은 다음과 같다. 우선 흑백 이미지 $A$에서 $R \times C$ 크기의 픽셀로 구성된 직사각형을 하나 선택한다. 이 직사각형은 좌측 상단 꼭짓점에 있는 픽셀의 위치 $(x, y)$ ($1 \le x \le N - R + 1$, $1 \le y \le M - C + 1$)에 의해 결정된다.
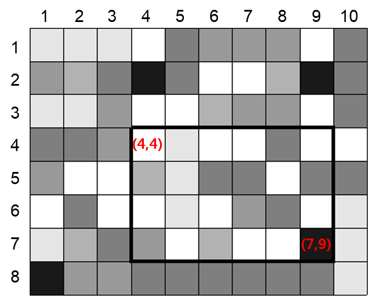
예를 들어 위 흑백 이미지를 $A$라고 하자. $A$에서 $4 \times 6$ 크기의 직사각형을 하나 선택했다고 하면 이 직사각형은 좌측 상단 꼭짓점인 $(4, 4)$에 의해 결정된다. (만약 좌측 상단 꼭짓점을 움직이면, 크기가 고정되어 있으므로, 직사각형도 같이 움직일 것) 이 직사각형의 우측 하단 꼭짓점은 $(7, 9)$인데, 이는 $(4 + 4 - 1, 4 + 6 - 1)$과 같다.
이제 이 직사각형과 사진 $B$가 비슷한지를 판단하는데, 그 기준은 다음과 같다.
- 어떤 실수 $p$와 $q$가 모든 $1 \le i \le R$, $1 \le j \le C$에 대해 $p\cdotA[x + i - 1, y + j - 1] + q = B[i, j]$를 만족시키면, $A$에서 선택한 직사각형과 사진 $B$는 비슷하다.
이 판단 기준을 $A$에 있는 모든 $R \times C$ 크기의 직사각형에 대해 적용하여, $B$와 비슷한 직사각형의 개수를 세면 된다. 다시 말해 $1 \le x \le N - R + 1$, $1 \le y \le M - C + 1$를 만족하는 모든 $(x, y)$에 대해 위 판단 기준을 적용한 후, 비슷하다고 판단되는 $(x, y)$ 쌍의 수를 세면 된다. 참고로 크기가 같은 두 직사각형이 다르다는 것은 좌측 상단 꼭짓점의 좌표가 서로 다르다는 것으로, 직사각형 내부 픽셀의 밝기와는 관계가 없다.
여러분은 경근이를 도와 $A$에서 $B$와 비슷한 부분이 몇 개인지 구하는 프로그램을 작성해야 한다.
입력
첫 번째 줄에 흑백 이미지 $A$의 행의 수 $N$, 열의 수 $M$ ($1 \le N, M \le 10^{3}$)이 공백을 사이로 두고 주어진다.
다음 $N$개의 줄에는 $A$의 픽셀들에 대한 정보가 주어진다. 이 중 $i$ ($1 \le i \le N$)번째 줄에는 $M$개의 정수 $A[i, 1], A[i, 2], ..., A[i, M - 1], A[i, M]$이 공백을 사이로 두고 주어진다. 즉 $i$번째 줄에서 $j$번째로 주어지는 정수는 $A$의 $i$행 $j$열에 있는 픽셀의 밝기를 의미한다.
그 다음 줄에 흑백 이미지 $B$의 행의 수 $R$, 열의 수 $C$ ($1 \le R \le N$, $1 \le C \le M$)이 공백을 사이로 두고 주어진다.
다음 $N$개의 줄에는 $B$의 픽셀들에 대한 정보가 주어진다. 이 중 $i$ ($1 \le i \le R$)번째 줄에는 $C$개의 정수 $B[i, 1], B[i, 2], ..., B[i, C - 1], B[i, C]$이 공백을 사이로 두고 주어진다. 즉 $i$번째 줄에서 $j$번째로 주어지는 정수는 $B$의 $i$행 $j$열에 있는 픽셀의 밝기를 의미한다.
주어지는 모든 픽셀 밝기는 0 이상 65,535 이하의 정수임이 보장된다.
출력
$A$에서 $B$와 비슷한 부분의 개수를 출력한다.
부분문제
| 부분문제 | 점수 | N, M |
|---|---|---|
| 1 | 33 | ≤ 102 |
| 2 | 68 | ≤ 103 |
입출력 예제
예제 1
입력
4 4
1 2 3 4
2 1 4 3
3 4 1 2
4 3 2 1
2 2
5 6
6 5
출력
5
예제 2
입력
5 5
9 2 5 4 3
6 8 2 0 2
4 3 6 4 3
7 2 3 4 8
8 2 4 6 7
3 3
77 77 77
77 77 77
77 77 77
출력
9
두 번째 예제의 경우 $p = 0, q = 77$이면 모든 부분이 비슷하다고 판별된다.