Random signals Batch 컴파일 명령

2차원 세상에는 1에서 N까지의 번호가 붙은 N개의 신호소가 있다. 신호소 i는 어떤 좌표 (x_i, y_i)를 중심으로 하는 원 영역에 신호를 보낼 수 있는데, 신호소에 들어오게 되는 전력량에 따라 그 세기와 반경이 달라진다. 정확히는 신호소 i는 (i, 1), ..., (i, M_i)로 이름 붙여진 M_i개의 서로 다른 신호를 보낼 수 있다. 신호 (i, j)는 r_i, j의 반경을 가지는 세기 s_i, j의 신호이며, w_i, j이상의 전력이 신호소 i에 들어오게 될 때 무조건적으로 신호를 보내게 되어 있다.

어떤 좌표 (x, y)에 전해지는 신호의 세기는 현재 존재하는 신호들 중에서 (x, y)를 포함하는 신호들 중 세기가 가장 큰 신호의 세기가 된다. 정부는 아래의 값 A가 신호가 세상에 퍼진 정도를 나타낼 수 있다고 생각한다.

<big> (신호 세기 s)  ×  (신호 세기가 s인 부분의 넓이)</big>

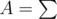
그리고 얼마 전부터 정부는 정책적으로 신호소 i에 들일 전력량을 매일 [L_i, U_i] 구간의 정수 중 하나를 동일한 확률로 선택한다. 이 때 A의 기댓값을 구하여 보자.

입력 형식

첫 번째 줄에 신호소의 개수를 의미하는 자연수 N (1 ≤ N ≤ 20)이 주어진다.

다음에는 N개의 신호소에 대한 정보가 주어진다. 각 신호소 마다 첫 번째 줄에는 다섯 개의 정수 x, y ( - 10⁴ ≤ x, y ≤ 10⁴), M (1 ≤ M ≤ 20), L, U (1 ≤ L ≤ U ≤ 10⁴)가 공백으로 구분되어 주어지고 다음 M개의 줄에는 세 개의 정수 r ,s ,w (1 ≤ r, s, w ≤ 10⁴)가 공백으로 구분되어 주어진다.

쉬운 문제에서는 모든 신호소에 대해 M = 1인 입력이 주어진다.

어려운 문제에서는 별 다른 제약이 없다.

출력 형식

A의 기댓값을 출력한다. 정답과의 절대오차 혹은 상대오차가  10^-8이하인 경우 정답으로 인정된다.