사다리꼴 Batch 컴파일 명령

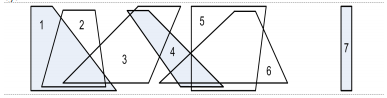
임의로 고른 두 개의 수평선을 고려해 봅시다. 이 두 선 사이의 사다리꼴 $T_{i}$은 아래 그림과 같이 위의 줄에 두 개, 아래 줄에 두 개의 점이 있습니다. 편의상 $T_{i}$의 좌측 상단의 점을 $a_{i}$, 우측 상단의 점을 $b_{i}$, 좌측 하단의 점을 $c_{i}$, 우측 하단의 점을 $d_{i}$로 나타냅시다. 사다리꼴들의 부분집합 $S$는 그 원소인 두 사다리꼴이 교차하지 않는다면 "독립적"이라고 합니다.

해야 할 일

사다리꼴들의 부분집합 중 최대 독립 집합의 크기(원소의 수가 가장 많은 집합의 원소의 수)와, 이 크기를 가지는 독립 집합들의 수를 30013으로 나눈 나머지를 구하는 프로그램을 작성하세요.

입력 형식

첫 번째 줄에는 사다리꼴의 수 $N$이 주어집니다. 다음 $N$개 줄에는 4개의 정수 $a_{i}, b_{i}, c_{i}, d_{i}$가 공백을 사이로 두고 주어집니다. 어떤 두 사다리꼴도 같은 점을 공유하지 않습니다.

출력 형식

최대 독립 집합의 크기와 이 크기를 가지는 부분집합들의 수를 30013으로 나눈 나머지를 공백을 사이로 두고 출력합니다.

제약 조건

• $1 \le N \le 100,000.$
• $1 \le a_{i}, b_{i}, c_{i}, d_{i} \le 1,000,000,000.$
• 최대 독립 집합의 크기만 정확하게 구했다면 해당 테스트 케이스의 40%에 해당하는 점수를 받을 수 있습니다.
• 40%의 테스트 데이터에 대해 $N \le 5,000.$

입출력 예제

위의 그림은 입력 예제를 알아보기 쉽게 하기 위하여 그린 것으로 정확하지는 않습니다. 사다리꼴의 윗변과 아랫변의 위치가 약간씩 바뀌었습니다.