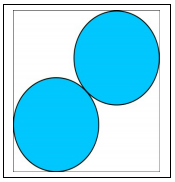
두 개의 원 Batch 컴파일 명령

$N$개의 정점으로 구성된 볼록다각형이 있습니다. 우리는 두 개의 원이 이 볼록다각형에 서로 겹치지 않고 내접할 수 있도록 하는 최대 반지름 $R$을 구하고자 합니다.

입력 형식

첫 번째 줄에 정점의 수 $N$이 주어집니다. 다음 $N$개 줄에 $i$번째 점의 좌표를 나타내는 두 정수 $x_{i}$와 $y_{i}$가 공백을 사이로 두고 주어집니다.

출력 형식

첫 번째 줄에 $R$을 소수점 아래 셋째 자리까지 출력합니다. 최대 $0.001$의 절대 오차만 허용됩니다.

제약 조건

• $3 \le N \le 5,0000.$
• $-10^7 \le x_{i} \le 10^7.$
• $-10^7 \le y_{i} \le 10^7.$
• 정점들은 시계반대방향으로 주어집니다.
• 10%의 테스트 데이터에 대해 $N = 3.$
• 40%의 테스트 데이터에 대해 $N \le 250.$

예제 1

입력

4
0 0
1 0
1 1
0 1

출력

0.293

예제 2

입력

4
0 0
3 0
3 1
0 1

출력

0.500

예제 3

입력

6
0 0
8 0
8 6
4 8
2 8
0 4

출력

2.189

참고

첫 번째 예제를 그림으로 나타내자면 아래와 같습니다.

이 때 두 원의 중심은 정사각형의 대각선 위에 있어야 하며, 반지름은 아래와 같이 계산됩니다.

$$\frac{ \sqrt{2} }{2 \times (1+\sqrt{2})} \approx 0.293$$