Tapestries Batch Compilation commands

An exhibition of tapestries is opening in Byteotian Museum of Fine Arts. The main exhibition room, viewed from top, is a polygon (not necessarily convex). A tapestry is hanged on each wall of the room, each tapestry taking all the area of its wall.

A lamp has been installed in the room in order to illuminate the exhibition. The lamp is glowing uniformly in all directions. However, while some of the tapestries have to be flooded with light, others cannot be exposed to strong light.

Byteasar, the curator, has been moving the lamp around the room, but so far he is not satisfied with the results. Now he is terrified by the prospect of moving the tapestries around instead - this would require much effort, and the exhibition is to open soon. Perhaps you will be able to tell him if his attempts are doomed or not?

Your task is to determine if there is such a spot that placing the lamp in it satisfies the following:

• each wall is to be either completely illuminated or completely shaded, as required by the tapestry hanging on it; there can be no wall that is partly illuminated and partly shaded;
• if the lamp is located exactly on the wall or its extension, this wall is not illuminated;
• the lamp can neither be switched off nor taken away from the room; it has to be on while located (strictly) inside the room (i.e., it cannot be placed in a corner or on any wall).

Input

There is a single integer $t$ ($1 \le t \le 20$) in the first line of the standard input, denoting the number of data sets. The following lines describe these data sets.

The first line of a single description holds a single integer $n$ ($3 \le n \le 1,000$), denoting the number of walls in the main exhibition room. Then the following n lines specify the room's shape. Each of those lines contains a pair of integers $x_{i}$ and $y_{i}$ ($-30,000 \le x_{i}, y_{i} \le 30,000$ for $i=1,2,\cdots,n$), separated by a single space, denoting the coordinates of the room's corner or, in other words, the vertex of corresponding polygon. The vertices are given clockwise.

The next $n$ lines specify the tapestries' requirements. Each of those lines contains a single letter, S or C, denoting that the wall has to be illuminated or shaded, respectively. The letter in the $i$-th of these lines (for $1 \le i \le n-1$) regards the wall between the $i$-th and the $(i+1)$-th vertex. The letter in the last of these lines regards the wall between the last and the first vertex.

The polygon depicting the room's shape has no self-crossings, i.e., with the exception of successive sides, which share a common vertex, no two sides of the polygon share a common point. Furthermore, no three vertices of the polygon are collinear.

In tests worth 40% of all points $n \le 20$ holds. Furthermore, in tests worth 10% of all points all the walls have to be illuminated.

Output

For each data set your program should print to the standard output a single line containing a single word:

• TAK (Polish for yes) if the lamp can be placed so as to satisfy all aforementioned requirements, or
• NIE (Polish for no) otherwise.

Example

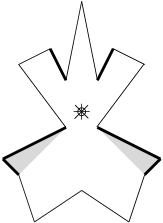
In the figures below the examples, the thick sides denote the walls that have to be shaded while the remaining sides - the walls that have to be illuminated. The figure for the first example shows a correct placement of the lamp.

For the input data:

1
16
5 -3
4 -4
3 -7
0 -5
-3 -7
-4 -4
-5 -3
-1 -1
-4 3
-2 4
-1 2
0 7
1 2
2 4
4 3
1 -1
C
S
S
S
S
C
C
S
S
C
S
S
C
S
S
C

the correct result is:

TAK

For the input data:

2
3
0 0
0 1
1 0
S
C
S
3
0 0
0 1
1 0
S
S
S

the correct result is:

NIE
TAK