관광 Batch 컴파일 명령

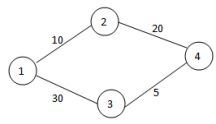
지학이가 운영하는 여행 회사는 관광객들을 위한 도시 투어를 조직하고자 합니다. 이 도시는 연결 그래프로 나타낼 수 있습니다. 각 노드는 관광지를 나타내고, 각 간선은 양방향 도로를 나타냅니다. 불운하게도, 모든 도로가 좋은 것은 아닙니다. 몇 개의 도로는 교통 체증 등의 이유로 별로 좋지 않을 수도 있습니다. 지학이는 관광객들이 도로 사정 때문에 실망하는 것을 원하지 않기 때문에, 가장 좋은 경로를 찾고자 합니다. 지학이는 각 도로에등급을 매깁니다. 좋은 도로일수록 등급이 높습니다. 지학이는 또한 "경로의 등급"이라는 것을 정의하는데, 이것은 해당 경로 위의 간선들의 등급들 중 가장 작은 등급을 의미합니다. 아래 그림은 4개의 관광지와 4개의 도로를 그래프로 나타낸 것입니다.

그래프의 각 간선에는 도로의 등급을 나타내는 값이 적혀 있습니다. 예로 들어, 간선 $(1, 2)$ (1과 2를 잇는 간선)의 등급은 10이고, 간선 $(3, 4)$의 등급은 5입니다. 경로 $1-2-4$의 등급은 $(1, 2)$와 $(2, 4)$의 등급 중 최소이므로 $\min\{10, 20\} = 10$이 됩니다. 이와 같이, 경로 $1-2-4-3$의 등급은 $(1, 2)$, $(2, 4)$, $(3, 4)$의 등급들 중 최소이므로 $\min\{10, 20, 5\} = 5$가 됩니다.

1번 노드는 여행객들이 머무르는 호텔입니다. 목적지 $X$가 주어질 때, 지학이는 1번 노드에서 출발하여 $X$번 노드에 도착하는 모든 가능한 경로들 중 등급이 가장 높은 경로를 찾고 싶습니다.

예를 들어, 그들이 4번 노드에 방문하고 싶다고 가정해 봅시다. 위의 예제에 따르면, 1번 노드에서 출발하여 4번 노드에 도착하는 모든 가능한 경로들 중 가장 높은 등급을 가지는 경로는 $1-2-4$이며, 이 때 등급은 10입니다. 반면, 만약 그들이 4번 노드 대신 3번 노드를 방문하고 싶어한다면, 가장 높은 경로의 등급은 30입니다.

더욱이, 지학이는 하나의 목적지까지 가는 경로의 최대 등급을 아는 데 만족하지 않습니다. 지학이는 마음 속에 목적지들의 목록을 가지고 있어서, 각 목적지마다 최대 등급을 알고 싶어 합니다. 다시 말해서, $Q$개의 관광지 $X_{1}, X_{2}, \cdots, X_{Q}$가 주어질 때, 지학이는 1번 노드와 $X_{1}$번 노드 사이의 최대 등급, $1$번 노드와 $X_{2}$번 노드 사이의 최대 등급, ..., 을 알고자 합니다.

입력 형식

첫 번째 줄에는 관광지의 수 $V$, 간선의 수 $E$와 목적지의 수 $Q$가 주어집니다. 관광지들에는 1번부터 $V$번까지의 번호가 붙어 있으며 이 중 1번은 호텔입니다. 다음 $E$개 줄에는 간선의 정보를 나타내는 세 정수 $v_{1}$, $v_{2}$, $q$가 주어지는데, 이는 이 도로가 $v_{1}$번 관광지와 $v_{2}$번 관광지를 연결하며 등급은 $q$ ($0 \le q \le 200,000$)임을 의미합니다. 다음 $Q$개 줄에는 지학이가 마음 속에 담아 둔(?) 관광지의 번호 $X$가 한 줄에 하나씩 주어집니다. 이 때 $X \neq 1$을 만족합니다. (1번은 호텔이므로)

출력 형식

주어지는 각 목적지마다 최대 등급을 한 줄에 하나씩 출력합니다.

서브태스크

1. (4점) 도로들은 연결된 단순 사이클을 형성합니다. 다시 말해, 모든 노드들은 정확히 2개의 간선과 연결되어 있습니다. $V \le 100; E \le 100; Q \le 50$.
2. (5점) 도로들은 일반적인 연결 그래프를 형성합니다. $V \le 500; E \le 4,000; Q \le 100$.
3. (6점) 도로들은 일반적인 연결 그래프를 형성합니다. $V \le 50,000; E \le 100,000; Q \le 10,000$.
4. (10점) 도로들은 일반적인 연결 그래프를 형성합니다. $V \le 500,000; E \le 5,000,000; Q \le V-1$.

예제