전봇대 Batch 컴파일 명령

일직선상에 $N$개의 전봇대가 한 줄로 서있다. 편의상, 일직선을 $x$-축이라 하고, 전봇대가 서 있는 위치 $x_{0}, x_{1}, \cdots, x_{N-1}$은 $x$-축 상의 $x$-좌표라고 하자. $x_{0}$는 항상 0이고 $x_{i}$($i \ge 1$)는 양의 정수라고 가정한다.

이 전봇대들을 이웃한 두 전봇대 사이의 거리가 모두 일정하도록 일부 전봇대들을 옮기려고 한다. 이때 이동해야하는 전봇대들의 거리의 합이 최소가 되도록 해야 한다. 단, $x_{0}$에 위치한 전봇대는 움직일 수 없고, 이동하는 전봇대들은 정수 좌표 위치로만 이동 가능하다.

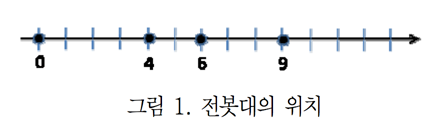
예를 들어, 아래의 그림 1과 같이 전봇대가 주어져 있다고 하자.

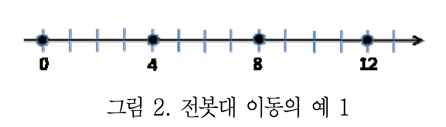
이 경우 그림 2에서와 같이 $x$-좌표 6과 9에 위치한 전봇대를 각각 $x$-좌표 8과 12인 곳으로 이동하면, 모든 이웃한 전봇대들의 거리는 4로 같고 전봇대의 이동 거리의 합은 5이다.

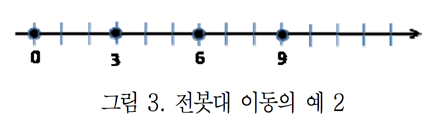
하지만 그림 3과 같이 $x$-좌표 4에 위치한 전봇대만을 $x$-좌표 3인 곳으로 이동하면, 이웃한 전봇대들의 거리는 모두 3이고 전봇대의 이동 거리의 합은 1이다.

전봇대들의 위치 $x_{0}, x_{1}, \cdots, x_{N-1}$이 주어지면, 모든 이웃한 전봇대들의 거리가 같도록 전봇대들을 이동할 때($x_{0}$에 위치한 전봇대는 고정), 이동 거리의 합이 최소가 되도록 하는 프로그램을 작성하시오.

수행시간은 1초를 넘을 수 없다. 메모리 제한은 32MB이다.

입력 형식

입력의 첫 줄은 전봇대의 수 $N$ ($1 \le N \le 100,000$)이 주어진다. 두 번째 줄에는 전봇대의 위치를 나타내는 $N$개의 서로 다른 $x$-좌표 $x_{i}$($i = 0, \cdots, N-1$)가 빈칸을 사이에 두고 오름차순으로 주어진다. $x_{i}$는 정수이고, $0 \le x_{i} \le 1,000,000,000$ 이다.

출력 형식

출력은 단 한 줄이며, 모든 이웃한 전봇대들의 거리가 같도록 전봇대들의 이동거리 합의 최솟값을 출력한다.

유의 사항

중간 계산 결과와 출력할 값이 32비트 정수형 범위를 벗어날 수 있으니 64비트 정수형을 이용 할 것을 권장한다.

부분문제의 제약 조건

• 부분문제 1: 전체 점수 100점 중 11점에 해당하는 데이터에 대해 $N \le 50$이고 $x_{N-1} \le 100,000$이다.
• 부분문제 2: 전체 점수 100점 중 21점에 해당하는 데이터에 대해 $N \le 1,000$이고 $x_{N-1} \le 100,000$이다.
• 부분문제 3: 전체 점수 100점 중 31점에 해당하는 데이터에 대해 $N \le 10,000$이고 $x_{N-1} \le 1,000,000,000$이다.
• 부분문제 4: 전체 점수 100점 중 37점에 해당하는 데이터에 대해 추가적인 제약 조건은 없다.

입력과 출력의 예