수족관 1 Batch 컴파일 명령

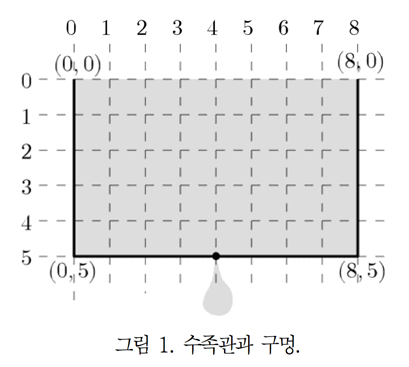
아래 그림 1은 수족관을 앞에서 본 모양이다. 이 수족관에는 물이 가득 차 있다. 만약 수족관 밑바닥(수평선분)에 구멍을 하나 뚫으면, 구멍을 통해 수족관의 물이 빠지게 된다.

그림 1의 수족관의 경계는 4개의 꼭짓점으로 표현된다. 각 꼭짓점의 위치는 세로줄 번호와 가로줄 번호로 나타낸다. 세로줄은 왼쪽에서 오른쪽으로 0번부터 차례로 증가하는 번호를 붙이고, 가로줄은 위부터 아래로 0번부터 차례로 증가하는 번호를 붙인다. 이웃한 두 세로줄 사이의 거리와 이웃한 두 가로줄 사이의 거리는 모두 1이다. 그래서 왼쪽 위에 있는 꼭짓점의 위치는 (세로줄 번호, 가로줄 번호) = (0, 0)이 되고, 이 꼭짓점부터 시계반대방향으로 수족관의 경계를 따라가면서 만나는 꼭짓점들의 위치는 차례로 (0, 5), (8, 5), (8, 0)이 된다.

수족관의 바닥을 나타내는 수평선분에 구멍이 있다면, 그 수평선분이 위치한 가로줄보다 위쪽에 있으면서 중력에 따라 구멍으로 흘러 들어갈 수 있는 위치에 있는 물은 모두 그 구멍을 통해 외부로 배출된다. 따라서 그림 1의 물은 바닥의 구멍을 통해 남김없이 모두 빠진다.

수족관에 담긴 물의 양은 물이 차지하는 면적과 일치하는 양이다. 물의 양의 단위는 L(리터)이다. 따라서 그림 1에서 가득 담긴 물의 양은 물이 차지하는 면적과 동일한 40L이다.

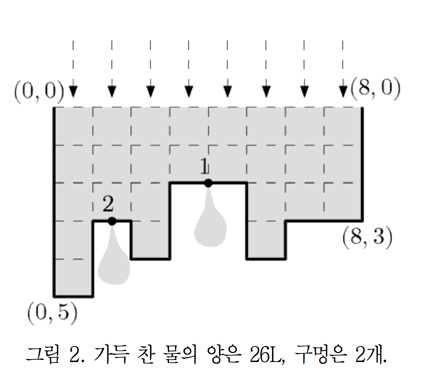
그림 2처럼 수족관의 바닥이 복잡할 수도 있다.

수족관의 바닥은 수평선분과 수직선분이 번갈아 여러 번 나타나는 형태이다. 또한 그림 2처럼 수족관 위에서 수직방향으로 수족관 바닥을 보았을 때, 수족관의 바닥이 모두 보이는 (즉, 모든 수평선분이 보이는) 형태이다.

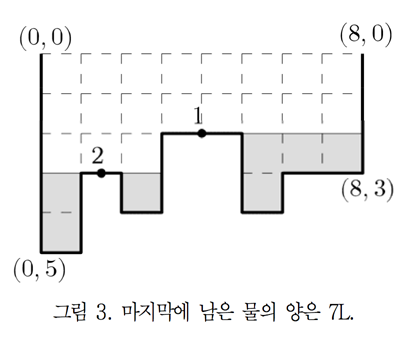
구멍은 항상 수평선분에만 존재하며, 수평선분의 한 가운데에 위치한다. 그리고 하나의 수평선분에는 최대 하나의 구멍만 존재할 수 있다. 그림 2에는 2개의 구멍(1번 구멍과 2번 구멍)이 있다. 이 구멍들을 통해 물을 빼면, 그림 3과 같이 빠져나가지 못한 물이 7L 남게 된다.

입력 형식

입력의 첫 줄은 수족관의 경계에 있는 꼭짓점의 개수 $N$ ($4 \le N \le 5,000$)이 주어진다. $N$은 짝수이다. 수족관의 경계는 항상 꼭짓점 (0, 0)부터 시작한다. 그리고 마지막 꼭짓점은 (A, 0)의 형태로 끝난다. 즉, 시작 꼭짓점과 마지막 꼭짓점의 가로줄 번호는 항상 0이다. 수족관의 경계를 이루는 변은 꼭짓점 (0, 0)부터 시작하는 데, 수직선분으로 시작하여 수평선분과 수직선분이 번갈아가며 반복되다 수직선분으로 끝난다. 따라서 수직선분이 수평선분보다 항상 하나 더 많다. 두 번째 줄부터 $N$개의 줄에는 수족관 경계에 있는 $N$개의 꼭짓점의 세로줄 번호와 가로줄 번호가 빈칸을 사이에 두고 각 줄에 하나씩, 첫 꼭짓점 (0, 0)부터 시계반대방향을 따라 차례로 주어진다. 세로줄과 가로줄 번호의 범위는 0 이상 40,000 이하의 정수이다. 다음 줄에는 수족관의 수평선분에 위치한 구멍의 개수 $K$ ($1 \le K \le N \div 2$)가 자연수로 주어진다. 다음 $K$개의 줄에는 각 구멍이 존재하는 수평선분의 양 끝 꼭짓점 위치를 나타내는 네 개의 값이 빈 칸을 사이에 두고 차례로 주어진다. 즉, 어떤 구멍이 위치한 수평선분의 정보가 $a$ $b$ $c$ $b$로 주어졌다면, 구멍이 위치한 수평선분은 꼭짓점 $(a, b)$와 꼭짓점 $(c, b)$를 연결한 선분이라는 의미이다. 항상 $a < c$ 이다.

출력 형식

출력은 단 한 줄이며, 구멍을 통해 물이 빠져 나간 후, 수족관에 남아 있는 물의 양을 0 이상의 정수로 출력한다.

부분문제의 제약 조건

• 부분문제 1: 전체 점수 100점 중 23점에 해당하는 데이터에 대해, $N = 6$, 세로줄, 가로줄의 번호 $\le 10$이다.
• 부분문제 2: 전체 점수 100점 중 19점에 해당하는 데이터에 대해 $N \le 10, K = 1,$ 세로줄, 가로줄의 번호 $\le 100$이다.
• 부분문제 3: 전체 점수 100점 중 22점에 해당하는 데이터에 대해, $K \le 100, $세로줄, 가로줄의 번호 $\le 500$이다.
• 부분문제 4: 전체 점수 100점의 36점에 해당하는 데이터에 대해 추가적인 제약 조건은 없다.

입력과 출력의 예