절취선 Batch 컴파일 명령
| 시간 제한 | 메모리 제한 | 제출 횟수 | 통과한 사람 수 | 비율 |
|---|---|---|---|---|
| 3000 ms | 256 MiB | 100 | 18 | 18.0% |
JOI군은 종이 공예가 취미이다. 오늘도 JOI군은 종이 공예 작품을 만드려고 한다.
우선, JOI군은 설계도에 따라서 한장의 직사각형 모양의 종이에 $N$개의 절취선을 인쇄했다. 각 절취선은 가로나 세로에 평행하다. 종이를 잘라낼 수 있는 모든 부분은 작품 내에서 부품으로 사용된다. 당연한 것이지만 부품수가 많을수록 작품의 제작이 어려워 진다. JOI군은, 모든 절취선을 따라 종이를 잘랐을 때, 종이가 몇 개의 부분으로 나뉘어지는가를 알고 싶다.
종이의 크기와, $N$개의 절취선에 대한 정보가 주어진다. 이러한 절취선을 따라 종이를 잘랐을 때, 종이가 몇부분으로 잘리는지 구하는 프로그램을 작성하여라.
입력 형식
표준 입력에서 다음 데이터가 다음의 데이터가 들어온다.
- 첫째 줄에는, $W$, $H$, $N$이 공백으로 구분되어 주어진다. $W$는 종이의 가로 길이, $H$는 종이의 세로 길이, $N$은 절취선의 갯수를 의미한다. 종이의 상하, 우하, 좌하, 우상 각각의 위치를 $(0, 0)$, $(W, 0)$, $(0, H)$, $(W, H)$로 나타낸다.
- 다음 N개의 줄에 i번째 줄에는 정수 $A_i, B_i, C_i, D_i$ ($0 \le A_i \le C_i \le W$, $0 \le B_i \le D_i \le H$)가 공백으로 구분되어 쓰여 있다. 이것은 $i$번째 절취선이 $(A_i, B_i)$와 $(C_i, D_i)$를 잇는 선분임을 나타낸다. 이 선은 종이중 한 변에 평행하다. 즉, $A_i=B_i$나 $C_i=D_i$ 중 정확히 하나만 성립한다. 또한, 모든 절취선에 대해서, 그 절취선을 연장한 직선상에 있는 다른 절취선이 점에서라도 만나는 경우는 없고, 종이의 변의 일부를 따라 절취선이 그려지는 경우도 없다.
출력 형식
첫 번째 줄에, JOI군이 모든 절취선을 따라 종이를 잘랐을 때, 종이가 몇 개의 부분으로 나누어지는지 그 수를 출력한다.
제한
모든 입력 데이터는 다음을 만족한다.
- $1 \le W \le 1\,000\,000\,000$
- $1 \le H \le 1\,000\,000\,000$
- $1 \le N \le 100\,000$
부분문제
Subtask 1 [5]
다음의 조건을 만족한다.
- $W \le 1\,000$
- $H \le 1\,000$
- $N \le 1\,000$
Subtask 2 [5]
다음의 조건을 만족한다.
- $N \le 1 000$
Subtask 3 [20]
공유점을 가지는 서로 다른 2개의 절취선의 쌍의 갯수는 100 000이하이다.
Subtask 4 [20]
절취선상의 임의의 점으로 부터, 종이의 한 변 까지 절단선을 따라 도달할 수 있다.
Subtask 5 [50]
추가 제한조건이 없다
예제 설명
| 입력 1 | 출력 1 |
|---|---|
| 10 10 5 6 0 6 7 0 6 7 6 2 3 9 3 2 3 2 10 1 9 8 9 |
4 |
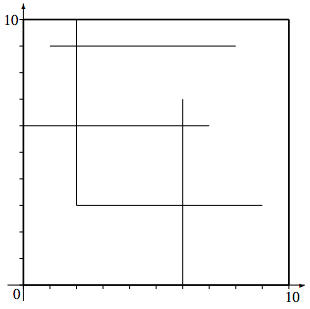
이 입력의 경우, 절취선은 다음과 같이 그려진다
여기서, 절취선에 의해 종이는 4부분으로 잘린다. 그리고, 이 입력은 Subtask 4의 조건을 만족한다.
| 입력 2 | 출력 2 |
|---|---|
| 13 7 28 1 1 4 1 1 1 1 3 2 2 3 2 2 2 2 3 1 3 2 3 3 2 3 6 4 1 4 6 3 6 4 6 5 1 8 1 5 1 5 6 6 2 7 2 6 2 6 5 7 2 7 5 6 5 7 5 8 1 8 6 5 6 8 6 9 1 12 1 9 1 9 2 9 2 10 2 12 1 12 2 11 2 12 2 10 2 10 5 9 5 10 5 9 5 9 6 11 2 11 5 11 5 12 5 12 5 12 6 9 6 12 6 |
5 |
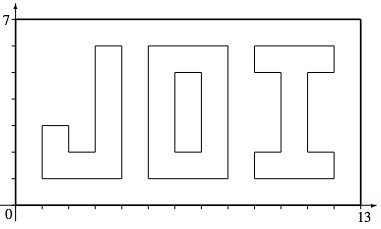
이 입력에서는, 절취선은 다음 그림과 같다.
여기서, 절취선에 의해 종이는 5부분으로 잘린다. 그리고, 이 입력은 Subtask 4의 조건을 만족하지 않는다.