즐거운 채소 기르기 Batch 컴파일 명령

승현이는 매년 자신의 텃밭에서 IOI풀(草)이라는 식물을 기르고 있습니다. 승현이의 밭은 동서로 $N$칸으로 나뉘어 있으며 각 칸에는 왼쪽에서부터 순서대로 $1$ 이상 $N$ 이하의 자연수 번호가 붙어 있습니다. 승현이는 $N$개의 IOI풀을 가지고 있고 각 풀은 한 칸에 한 포기씩 심겨져 있습니다. 이 중 $i$번 칸에 심겨 있는 풀은 봄이 되면 키가 $h_{i}$까지 늘어나며, 이것보다 크게는 자라지 않습니다.

봄이 되자 풀들이 어떻게 자라고 있는지 보러 간 승현이는, IOI풀들의 배치가 자신의 생각과 다르게 되어 있다는 것을 발견했습니다. IOI풀은 많은 햇빛을 필요로 하는 식물로, 임의의 IOI풀보다 키가 큰 IOI풀이 이보다 번호가 작은 칸에 1개 이상 있고 번호가 큰 칸에 1개 이상 있다면 이 IOI풀은 여름이 되기 전에 시들어버립니다. 즉 어느 IOI풀도 시들지 않게 하려면 아래 조건을 만족해야 합니다.

• $2 \le i \le N-1$을 만족하는 임의의 정수 $i$에 대해 다음 두 가지 조건 중 적어도 하나는 만족되어야 합니다.
  • $1 \le j \le i-1$을 만족하는 모든 정수 $j$에 대해 $h_{j} \le h_{i}$
  • $i+1 \le k \le N$을 만족하는 모든 정수 $k$에 대해 $h_{k} \le h_{i}$

IOI풀은 그 이름과 같이 매우 고가이므로 승현이는 어떤 풀도 시들지 않도록 풀들을 다시 정렬하기로 결정했습니다. IOI풀은 매우 크고 민감하기 때문에 승현이는 인접한 두 IOI풀을 교체할 수밖에 없습니다. 즉, 승현이는 한 번의 조작으로 $i$ ($1 \le i \le N-1$)번 칸의 IOI풀과 $(i+1)$번 칸의 IOI풀을 교체할 수 있습니다. 여름이 다가오면 풀들이 시들 가능성이 높아지므로, 승현이는 가능한 한 빨리 정렬하기를 원합니다. 모든 IOI풀들이 죽지 않기 위해 필요한 가장 적은 조작 횟수를 구하세요.

해야 할 일

승현이의 밭의 크기와 각 IOI풀의 높이가 주어졌을 때, 모든 IOI풀들이 시들지 않도록 정렬하는 데 필요한 작업 횟수의 최솟값을 출력하는 프로그램을 작성하세요.

입력 형식

표준 입력으로 아래 입력을 받습니다.

• 첫 번째 줄에 승현이의 밭의 칸 수 $N$이 주어집니다.
• 다음 $N$개 줄에는 IOI풀들의 높이에 관한 정보가 주어집니다. 이들 중 $i$ ($1 \le i \le N$)번째 줄에는 정수 $D_{i}$가 주어집니다. $D_{i}$는 $i$번 칸에 심겨 있는 IOI풀의 봄 때의 키입니다.

출력 형식

표준 출력으로 승현이에게 필요한 최소 조작 횟수를 출력합니다.

제약 조건

모든 입력 데이터는 아래 조건을 만족합니다.

• $3 \le N \le 300,000$
• $1 \le D_{i} \le 1,000,000,000$

서브태스크

서브태스크 1 [10점]

• $N \le 8$

서브태스크 2 [20점]

• $N \le 20$

서브태스크 3 [15점]

• $N \le 5000$

서브태스크 4 [55점]

추가 제약 조건이 없습니다.

예제

입력	출력
6 2 8 4 5 3 6	3

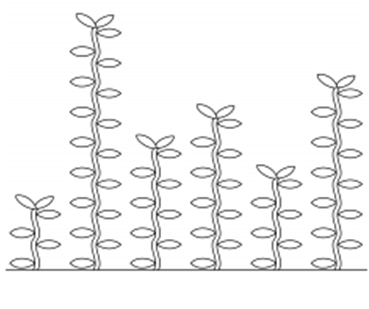
처음 승현이의 밭에 심겨 있는 IOI풀들은 아래와 같이 배치되어 있습니다.

예를 들어 아래와 같이 움직이면 3번만에 모든 IOI풀들이 시들지 않도록 할 수 있습니다.

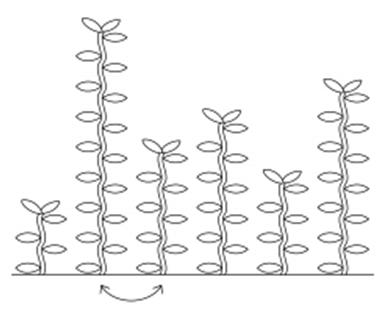
2번 칸의 IOI풀과 3번 칸의 IOI풀을 교환합니다.

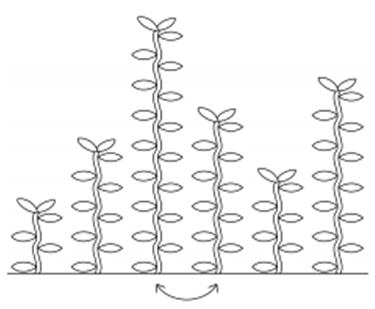
3번 칸의 IOI풀과 4번 칸의 IOI풀을 교환합니다.

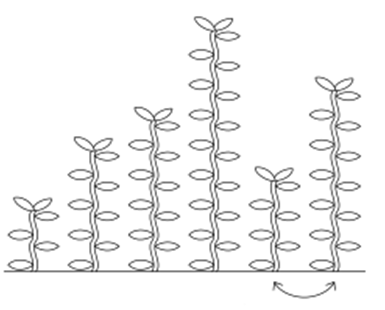
5번 칸의 IOI풀과 6번 칸의 IOI풀을 교환합니다.

잘 정렬되었습니다.

입력	출력
5 4 4 2 4 4	2

3번 칸의 IOI풀을 1번 칸 또는 5번 칸으로 옮기면 됩니다.

입력	출력
4 1 3 4 2	0