별자리 2 Batch 컴파일 명령

JOI군과 IOI군은 친구 사이입니다. 어느 날 JOI군은 IOI군과 함께 산 위에 있는 전망대에서 천체 관측을 하기로 했습니다.

전망대에서는 $N$개의 별을 관측할 수 있습니다. 각각의 별에는 1 이상 $N$ 이하의 자연수 번호가 붙어 있으며, 각각의 별들은 빨강색, 파랑색, 노랑색 중 하나의 색을 띱니다.

이 전망대에서 관측된 별은 좌표 평면 상의 점으로 표시됩니다. 이 좌표평면에서 각 $i$ ($1 \le i \le N$)에 대응하는 점은 $P_{i} (X_{i}, Y_{i})$입니다. 좌표평면 상의 점 $P_{1}, \cdots, P_{N}$은 그 위치가 서로 다르며, 어떤 세 점도 같은 직선 위에 있지 않습니다.

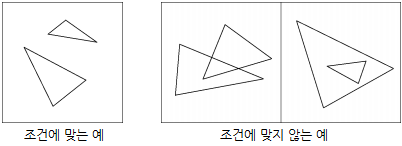
JOI군과 IOI군은 JOIOI 자리라는 별자리를 만들기로 했습니다. 먼저 두 사람은 빨강색, 파랑색, 노랑색이 세 개의 별을 연결한 삼각형을 사용하기로 합니다. 이러한 삼각형을 좋은 삼각형이라고 부릅니다.

두 사람은 다음 조건을 만족하는 좋은 삼각형 한 쌍 (순서는 관계 없습니다)을 JOIOI 자리의 후보로 두기로 합니다.

• 2개의 좋은 삼각형 (삼각형의 둘레 및 내부)에 공유하는 점이 없습니다. 즉 두 개의 좋은 삼각형이 겹치거나 한 삼각형이 다른 삼각형에 포함된 경우는 없습니다.

JOI군과 IOI군은 JOIOI자리의 후보로 간주되는 삼각형이 몇 개인지 셀 수 있습니다. 그러나 JOIOI 자리의 후보를 구성하는 6개의 별이 같아도 삼각형으로 묶는 방법이 다르다면 다른 후보로 취급합니다.

해야 할 일

전망대에서 관측된 별의 정보가 주어질 때, JOIOI자리의 후보 수를 출력하는 프로그램을 작성하세요.

입력 형식

표준 입력으로 아래 데이터를 받습니다:

• 첫 번째 줄에는 정수 $N$이 주어집니다. 이것은 전망대에서 관측된 별의 개수가 $N$임을 나타냅니다.
• $N$개 줄이 주어집니다. 이 중 $i$번째 줄 ($1 \le i \le N$)에는 세 개의 정수 $X_{i}, Y_{i}, C_{i}$가 공백을 사이로 두고 주어집니다. 이것은 $i$번 별의 좌표가 $P_{i} (X_{i}, Y_{i})$임을 나타내고, $C_{i}$는 $i$번 별의 색을 나타냅니다. $i$번 별의 색은 $C_{i}$가 0이면 빨강색, 1이면 파랑색, 2이면 노랑색입니다.

출력 형식

표준 출력에 JOIOI 자리의 후보의 수를 출력합니다.

제약 조건

모든 입력은 아래 조건을 만족합니다:

• $6 \le N \le 3,000$
• $-100,000 \le X_{i} \le 100,000$
• $-100,000 \le Y_{i} \le 100,000$
• $0 \le C_{i} \le 2$
• 어떤 색의 별도 1개 이상 존재합니다.
• $P_{i} \neq P_{j}$ ($1 \le i < j \le N$)
• $P_{i}, P_{j}, P_{k}$는 같은 직선 상에 있지 않습니다. ($1 \le i < j < k\le N$)

서브태스크

서브태스크 1 [15점]

• $N \le 30$

서브태스크 2 [40점]

• $N \le 300$

서브태스크 3 [45점]

추가 제약 조건은 없습니다.

입출력 예제

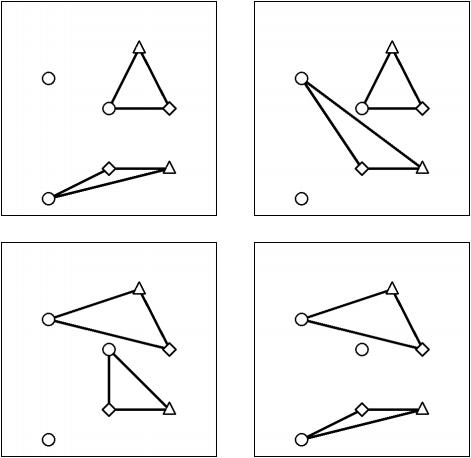
이 입력 예제에서 별들은 아래와 같이 배치됩니다. 이 그림에서 빨간색 별은 둥근 점으로, 파랑색 별은 마름모 형태의 점으로, 노랑색 별은 삼각형 모양의 점으로 나타냅니다.

이 입력 예제에서 JOIOI 자리의 후보는 다음 네 가지가 있습니다.