Mosaic Batch
| Time limit | Memory limit | # of submissions | # of submitted users | Solved # | Accepted user ratio |
|---|---|---|---|---|---|
| 1000 ms | 2048 MiB | 1068 | 137 | 91 | 66.42% |
Salma plans to colour a clay mosaic on a wall. The mosaic is an $N \times N$ grid, made of $N^2$ initially uncoloured $1 \times 1$ square tiles. The rows of the mosaic are numbered from $0$ to $N-1$ from top to bottom, and the columns are numbered from $0$ to $N-1$ from left to right. The tile in row $i$ and column $j$ ($0 \leq i < N$, $0 \leq j < N$) is denoted by $(i,j)$. Each tile must be coloured either white (denoted by $0$) or black (denoted by $1$).
To colour the mosaic, Salma first picks two arrays $X$ and $Y$ of length $N$, each consisting of values $0$ and $1$, such that $X[0] = Y[0]$. She colours the tiles of the topmost row (row $0$) according to array $X$, such that the colour of tile $(0,j)$ is $X[j]$ ($0 \leq j < N$). She also colours the tiles of the leftmost column (column $0$) according to array $Y$, such that the colour of tile $(i,0)$ is $Y[i]$ ($0 \leq i < N$).
Then she repeats the following steps until all tiles are coloured:
- She finds any uncoloured tile $(i,j)$ such that its up neighbor (tile $(i-1, j)$) and left neighbor (tile $(i, j-1)$) are both already coloured.
- Then, she colours tile $(i,j)$ black if both of these neighbors are white; otherwise, she colours tile $(i, j)$ white.
It can be shown that the final colours of the tiles do not depend on the order in which Salma is colouring them.
Yasmin is very curious about the colours of the tiles in the mosaic. She asks Salma $Q$ questions, numbered from $0$ to $Q-1$. In question $k$ ($0 \leq k < Q$), Yasmin specifies a subrectangle of the mosaic by its:
- Topmost row $T[k]$ and bottommost row $B[k]$ ($0 \leq T[k] \leq B[k] < N$),
- Leftmost column $L[k]$ and rightmost column $R[k]$ ($0 \leq L[k] \leq R[k] < N$).
The answer to the question is the number of black tiles in this subrectangle. Specifically, Salma should find how many tiles $(i, j)$ exist, such that $T[k] \leq i \leq B[k]$, $L[k] \leq j \leq R[k]$, and the colour of tile $(i,j)$ is black.
Write a program that answers Yasmin's questions.
Implementation Details
You should implement the following procedure.
std::vector<long long> mosaic(
std::vector<int> X, std::vector<int> Y,
std::vector<int> T, std::vector<int> B,
std::vector<int> L, std::vector<int> R)
- $X$, $Y$: arrays of length $N$ describing the colours of the tiles in the topmost row and the leftmost column, respectively.
- $T$, $B$, $L$, $R$: arrays of length $Q$ describing the questions asked by Yasmin.
- The procedure should return an array $C$ of length $Q$, such that $C[k]$ provides the answer to question $k$ ($0 \leq k < Q$).
- This procedure is called exactly once for each test case.
Constraints
- $1 \leq N \leq 200,000$
- $1 \leq Q \leq 200,000$
- $X[i] \in {0, 1}$ and $Y[i] \in {0, 1}$ for each $i$ such that $0 \leq i < N$
- $X[0] = Y[0]$
- $0 \leq T[k] \leq B[k] < N$ and $0 \leq L[k] \leq R[k] < N$ for each $k$ such that $0 \leq k < Q$
Subtasks
| Subtask | Score | Additional Constraints |
|---|---|---|
| 1 | $5$ | $N \leq 2; Q \leq 10$ |
| 2 | $7$ | $N \leq 200; Q \leq 200$ |
| 3 | $7$ | $T[k] = B[k] = 0$ (for each $k$ such that $0 \leq k < Q$) |
| 4 | $10$ | $N \leq 5000$ |
| 5 | $8$ | $X[i] = Y[i] = 0$ (for each $i$ such that $0 \leq i < N$) |
| 6 | $22$ | $T[k] = B[k]$ and $L[k] = R[k]$ (for each $k$ such that $0 \leq k < Q$) |
| 7 | $19$ | $T[k] = B[k]$ (for each $k$ such that $0 \leq k < Q$) |
| 8 | $22$ | No additional constraints. |
Example
Consider the following call.
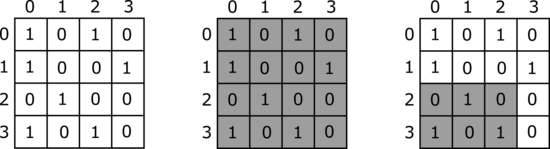
mosaic([1, 0, 1, 0], [1, 1, 0, 1], [0, 2], [3, 3], [0, 0], [3, 2])
This example is illustrated in the pictures below. The left picture shows the colours of the tiles in the mosaic. The middle and right pictures show the subrectangles Yasmin asked about in the first and second question, respectively.
The answers to the questions (that is, the numbers of ones in the shaded rectangles) are 7 and 3, respectively. Hence, the procedure should return $[7, 3]$.
Sample Grader
Input format:
N
X[0] X[1] ... X[N-1]
Y[0] Y[1] ... Y[N-1]
Q
T[0] B[0] L[0] R[0]
T[1] B[1] L[1] R[1]
...
T[Q-1] B[Q-1] L[Q-1] R[Q-1]
Output format:
C[0]
C[1]
...
C[S-1]
Here, $S$ is the length of the array $C$ returned by mosaic.
| File name | Size |
|---|---|
| mosaic.zip | 2.42 KiB |