배열 탈출 Batch 컴파일 명령

상수는 2차원 배열 $A[1..n][1..n]$ ($n \ge 2$, $n$은 자연수)을 가지고 있습니다. 이 배열의 각 원소는 1 이상 222 이하의 정수입니다.

배열을 가지고 놀던 상수를 본 승현이는, 질투심이 불타올라 상수를 $A[1][1]$에 가둬 버렸습니다! 최소한의 양심이 있던 승현이는 $A[n][n]$에 출구를 만들어 놓고 이 사실을 상수에게 알려줬습니다.

<small>[그림 1] $n = 4$라면 상수는 $A[1,1]$에 있고, 출구는 $A[4][4]$에 있습니다.</small>

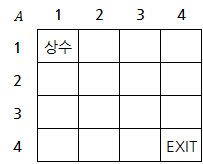
상수는 가능한 한 빨리 출구인 $A[n][n]$에 도달하고자 합니다. 상수가 $A[i][j]$에 있다고 가정했을 때, 상수는 최단 경로로 이동하기 위해 아래와 같은 조건을 만족하며 이동합니다.

1. $1 \le i, j < n$이라면, 상수는 $A[i][j+1]$ 또는 $A[i+1][j]$로만 건너갑니다.
2. $i = n, 1 \le j < n$이라면, $A[i][j+1]$로만 건너갑니다.
3. $1 \le i < n, j = n$이라면 $A[i+1][j]$로만 건너갑니다.
4. $i = j = n$인 경우 바로 출구로 갑니다.

<small>[그림 2] $n = 5$라고 가정합시다. (ㄱ)는 1번 조건을 만족하고, (ㄴ)는 2번 조건을 만족하며, (ㄷ)는 3번 조건을 만족합니다.</small>

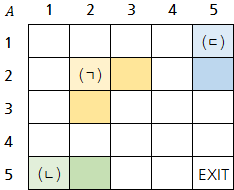
그러나 건너갈 때에도 제약이 따릅니다. 상수가 $A[a][b]$에서 $A[c][d]$로 건너가려면 $A[a][b] > A[c][d]$를 만족해야 합니다. 상수는 왜인지 이런 조건을 만족하면서 이동할 수 없을 것 같았습니다. 다행히도, 승현이가 상수를 배열에 가둬버리기 전에, 상수는 배열의 각 원소에 버튼을 만들어 놓아서, 이 버튼을 누르면 해당 원소의 값이 1 증가하도록 했습니다. (물론 상수는 자신이 위치해 있는 원소의 버튼만 누를 수 있습니다.) 이 버튼 덕분에, 상수는 항상 배열을 탈출할 수 있습니다!

<small>[그림 3] $n = 2$라고 가정합시다. $A[1][1] = 5 > A[1][2] = 2$이므로, 상수는 $A[1][1]$에서 $A[1][2]$로 건너갈 수 있습니다.
상수가 $A[1][1]$에서 $A[2][1]$로 건너가려면, $A[1][1]$에 있는 버튼을 두 번 눌러 $A[1][1]$의 값을 7로 만들면 됩니다.</small>

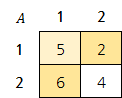
하지만 버튼을 한 번 누르는 데에는 1원의 비용이 듭니다. 상수는 돈을 가능한 한 적게 들이면서 배열을 탈출하고자 합니다. 상수를 도와주세요.

입력 형식

첫 번째 줄에 $n$이 주어집니다.

다음에 $n$개 줄이 주어집니다. 이 중 $i$($1 \le i \le n$)번째 줄에는 $n$개의 수 $A[i][1], A[i][2], \cdots, A[i][n-1], A[i][n]$이 공백을 사이로 두고 차례대로 주어집니다.

[주의] 입력이 아주 많으므로 C++에서 cin과 같은 입력을 사용하지 않는 것을 권장합니다. scanf를 사용해서 입력을 받아주세요. 아래 코드를 참조하세요. scanf 함수는 stdio.h에 있습니다.

int i, j;
scanf("%d", &n);
for(i = 1; i <= n; i++) {
    for(j = 1; j <= n; j++) {
        scanf("%d", &A[i][j]);
        // ...
    }
}

출력 형식

첫 번째 줄에 상수가 배열을 탈출하기 위해 들여야 할 최소 비용(원 단위)을 출력합니다.

부분문제

이 문제는 번호가 큰 부분문제가 번호가 작은 부분문제를 포함하므로, $k$번 부분문제에서 0점을 받으면 $k+1, \cdots, 4$번 부분문제는 채점하지 않고 0점 처리됩니다.

예제

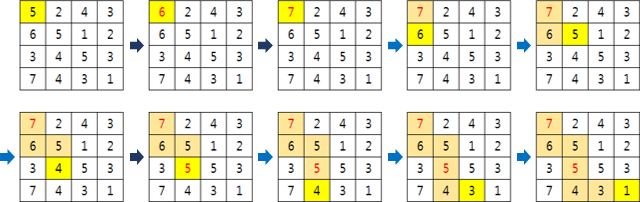
상수는 아래 그림과 같은 방법으로 탈출할 수 있습니다.

이렇게 하면 $A[1][1]$에서 2원, $A[3][2]$에서 1원의 비용이 들어 총 3원의 비용이 들게 되며, 이것이 최소입니다.