컴퓨터 네트워크 Batch
| 시간 제한 | 메모리 제한 | 제출 횟수 | 제출한 사람 수 | 해결한 사람 수 | 정답률 |
|---|---|---|---|---|---|
| 1000 ms | 64 MiB | 287 | 80 | 71 | 88.75% |
승현이의 학교 컴퓨터실에는 $N$개의 컴퓨터들이 있으며 그들은 단일한 네트워크를 형성하기 위해 케이블들로 연결되어 있습니다. 각 케이블은 두 개의 서로 다른 컴퓨터를 연결합니다. 어떤 두 컴퓨터의 쌍은 케이블로 바로 연결되어 있지 않을 수는 있지만, 모든 메시지는 항상 어떤 컴퓨터에서 다른 컴퓨터로 여러 개의 케이블로 연결된 중간 컴퓨터들을 거쳐서 전달될 수 있습니다. 메시지는 항상 최단 경로를 따라 이동합니다. 여기서 최단 경로란 경로 상의 중간 컴퓨터들의 개수(다시 말해, 메시지가 거치는 컴퓨터들 중 보내는 컴퓨터와 받는 컴퓨터를 제외한 컴퓨터의 수)가 최소화되는 경로를 말합니다.
이 교실에서 서로 다른 두 컴퓨터 $a$와 $b$를 사용하는 승현이와 상수는 그들의 컴퓨터 사이의 최단 경로를 결정하고 싶어합니다. 그들은 케이블들이 어떻게 연결되어 있는지 알 수는 없으나 모든 컴퓨터 쌍 사이에 메시지를 보내어 그 메시지가 방문하는 중간 컴퓨터들의 수를 계산할 수 있습니다.
하지만 승현이와 상수는 컴퓨터를 잘 다루지 못하므로 여러분에게 메시지를 너무 많이 보내지 않으면서 최단 경로를 결정해 내도록 도와주기를 요청합니다.
해야 할 일
허용된 것보다 더 많이 메시지를 전송하지 않으면서 $a$와 $b$ 사이의 최단 경로를 찾아 내는 프로그램을 작성하세요.
구현
여러분은 아래 파라미터가 주어지는 한 개의 함수 findRoute(N, a, b)를 작성해야 합니다:
- $N$ - 컴퓨터실 안에 있는 컴퓨터의 수입니다. (컴퓨터들에는 $1$ 이상 $N$ 이하의 정수 번호가 붙어 있습니다)
- $a$, $b$ - 승현이와 상수가 앉은 컴퓨터의 번호입니다. ($a \neq b$이고 $1 \le a, b \le N$)
여러분의 함수 findRoute는 함수 ping(i, j)를 호출할 수 있습니다. 이 함수는 서로 다른 두 컴퓨터의 번호 $i$와 $j$ ($i \neq j$이고 $1 \le i, j \le N$)를 인자로 받고 $i$에서 출발하여 $j$에 도착하는 메시지가 방문하는 중간 컴퓨터들의 수를 반환할 것입니다.
여러분의 함수 findRoute는 $a$에서 출발하여 $b$에 도착하는 메시지가 방문할 최단 경로를 표현해야 합니다. 이것은 반드시 함수 travelTo(k)를 반복적으로 호출하여 이행되어야 합니다. 이 함수는 메시지가 바로 다음에 이동할 컴퓨터의 번호 $k$ ($1 \le k \le N$)을 인자로 받습니다. 메시지는 $a$에서 시작하며, travelTo(k)가 호출될 때마다 $k$번 컴퓨터로 이동합니다.
여러분의 프로그램은 보통과 같은 제약 조건 (예: 시간 제한, 메모리 제한, 런타임 에러 금지, ..) 이외에도 아래와 같은 제약 조건을 만족해야 합니다.
findRoute가 종료될 때 메시지는 반드시 $b$에 있어야 합니다.- 최단 경로 상의 연속한 두 컴퓨터들은 반드시 케이블로 연결되어 있어야 합니다.
- 반드시 최단 경로로 이동해야 합니다.
- 함수
ping을 호출하는 횟수 $M$은 아래에 기술된 제한을 넘으면 안 됩니다. - 함수
ping과travelTo는 반드시 허용된 범위 안의 인자로 호출되어야 합니다.
예제
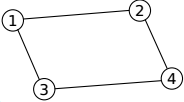
아래 예제를 고려해 봅시다. (원은 컴퓨터에, 줄은 케이블에 대응됩니다) 총 $N = 4$개의 컴퓨터가 있으며, 승현이와 상수는 컴퓨터 $a = 1$과 $b = 4$를 사용하고 있습니다.
첫 번째로 여러분의 함수
findRoute(4, 1, 4)
가 호출될 것입니다. 이 함수는 아래와 같이 동작할 수 있습니다.
ping(1, 4)가 호출되어 1이 반환됩니다. ping(1, 2)가 호출되어 0이 반환됩니다. ping(2, 4)가 호출되어 0이 반환됩니다.
이 정보는 1에서 출발하여 4에 도착하는 최단 경로가 $1 \rightarrow 2 \rightarrow 4$임을 결정하는 데 충분합니다. 이것은 아래와 같이 표현되어야 합니다.
travelTo(2)를 호출합니다. travelTo(4)를 호출합니다. findRoute가 종료됩니다.
채점 기준
모든 서브태스크에서 $2 \le N \le 1,000$이 성립합니다.
서브태스크 1 (25점)
- 어떤 두 컴퓨터 사이에도 정확히 한 개의 최단 경로가 있습니다.
- $M$은 $2N$ 이하여야 합니다.
서브태스크 2 (25점)
- $M$은 $N^2$ 이하여야 합니다.
서브태스크 3 (25점)
- $M$은 $4N$ 이하여야 합니다.
서브태스크 4 (25점)
- $M$은 $2N$ 이하여야 합니다.
실험
public.zip에 주어지는 예제 채점기는 표준 입력(stdin)으로부터 데이터를 입력받습니다. 입력의 첫 번째 줄은 반드시 네 개의 정수 $N, a, b$와 $M$의 최대 한도를 포함해야 합니다. 다음 $N$개 줄에는 케이블의 연결 형태를 나타내는 $N$개의 정수가 각각 주어집니다. 이들 중 $i$번째 줄의 $j$번째 수($i \neq j$)는 $i$에서 출발하여 $j$에 도착하는 최단 경로가 방문하는 중간 컴퓨터들의 수여야 합니다. $i = j$일 때의 값은 중요하지 않습니다.
다음 입력은 $M$의 제한이 100일 때 위의 예제를 나타냅니다.
4 1 4 100
0 0 0 1
0 0 1 0
0 1 0 0
1 0 0 0
채점기를 사용하기 위해서는 모든 파일들을 동시에 컴파일해야 합니다. 리눅스의 경우 run.sh 파일을 참고하시고, 윈도우에서 IDE로 작업하실 경우 한 프로젝트에 파일을 모두 넣은 뒤 컴파일해 주세요.
| 파일명 | 크기 |
|---|---|
| public.zip | 4.95 KiB |