경찰관과 강도 Batch
| 시간 제한 | 메모리 제한 | 제출 횟수 | 제출한 사람 수 | 해결한 사람 수 | 정답률 |
|---|---|---|---|---|---|
| 1500 ms | 256 MiB | 1512 | 198 | 135 | 68.18% |
중요: 이 문제는 대회 규정상 C로 채점할 수 없습니다. C로 제출할 시 컴파일 에러가 발생합니다. 반드시 C++로 채점하시기 바랍니다.
Bytemore 시에서 범죄 수준은 역대 최고를 달리고 있습니다. 모든 경범죄들을 통틀어 강도 사건은 매일매일 일어나고 있습니다. 그리고 그 범죄가 행해질 때, 항상 한 명의 순찰 경찰이 강도를 쫓아서 길모퉁이를 연결하는 좁은 골목길을 지나가야 합니다. 불행히도, 강도들은 경찰에게 잡히는 경우보다 탈출에 성공하는 경우가 많은데, 그들이 경찰보다 도시 지리를 더 잘 알기 때문입니다.
Bytemore 시의 경찰청(The Bytemore City Police Department, BCPD)은 범죄를 줄이기 위한 정상 회의를 준비하고 있습니다. 계획들 중 하나는 강도들을 쫓을 때 컴퓨터를 사용하는 것입니다. 이를 위해, BCPD는 도시의 정밀한 지도를 만들었습니다. 이제 그들은 추적 전략을 마련하기 위한 컴퓨터 소프트웨어가 필요합니다.
한 명의 강도를 쫓는 경찰관 한 명의 추적 문제는 아래와 같이 모델화됩니다.
- 경찰관은 순찰할 길모퉁이를 하나 고릅니다.
- 강도는 강도질을 할 길모퉁이를 하나 고릅니다. (그는 경찰관이 어디 있는지 알고 있습니다.) 이것은 아래에서 '시작점'이나 '출발점'을 고르는 과정입니다. 이 순간부터 경찰관과 강도는 서로가 어디에 있는지 항상 알고 있다고 가정합니다.
- 경찰관은 자신이 있는 길모퉁이와 이웃한 길모퉁이(현재 있는 길모퉁이와 골목길로 연결된 길모퉁이)로 가거나 기다릴(움직이지 않을) 수 있습니다.
- 강도는 자신이 있는 길모퉁이와 이웃한 길모퉁이로 이동해야 합니다. 강도는 경찰관과 다르게 기다릴 수 없습니다.
- 경찰관과 강도는 아래와 같은 상황 중 하나가 벌어지기 전까지 번갈아 가면서 이동합니다.
- 상황이 계속 반복됩니다. (여기서 '상황'이란 두 사람의 위치와 다음에 이동할 사람이 누구인지에 따라 정의됩니다) 이것은 강도가 영원히 잡히지 않을 수 있다는 것을 의미하며, 따라서 강도는 탈출합니다.
- 경찰관과 강도 둘 중 하나가 움직여서 같은 길모퉁이에서 만납니다. 이 상황에서 경찰관은 강도를 잡습니다.
해야 할 일
여러분은 도시의 지도가 주어질 때, 강도를 잡을 수 있는지 결정하고, 만약 잡을 수 있다면, 각 상황마다 경찰관이 어디로 움직일지 결정하는 프로그램을 작성해야 합니다.
여러분의 프로그램은 반드시 강도가 항상 최선을 다해 도망친다고 가정해야 합니다.
구현
여러분은 두 개의 함수를 구현해야 합니다.
start(N, A)- $N$ : 길모퉁이의 수 (길모퉁이들은 $0$ 이상 $N-1$ 이하의 정수 번호를 가집니다)
- $A$ : 골목길들을 표현하는 이차원 배열입니다. $0 \le i, j \le N-1$을 만족하는 두 $i, j$에 대해, 만약 $i$와 $j$가 한 골목길로 연결되어 있다면 $A[i,j]$는
true이고 그렇지 않다면 $A[i,j]$는false입니다. 모든 골목길은 양방향 통행이 가능하고 (즉 모든 가능한 $i, j$에 대해 $A[i, j] = A[j, i]$) 자기 자신을 연결하는 골목길은 없습니다. (즉 모든 가능한 $i$에 대해 $A[i, i]$는false입니다) 또한, 여러분은 어떤 길모퉁이에서 여러 개의 골목길들을 따라 다른 모든 길모퉁이로 이동할 수 있다고 가정해도 좋습니다. - 만약 경찰이 주어진 도시에서 강도을 잡을 수 있다면,
start는 경찰이 순찰하기로 결정할 길모퉁이의 번호를 반환해야 합니다. 그렇지 않다면 (잡을 수 없다면), $-1$을 반환해야 합니다.
nextMove(R)은 현재 강도가 있는 길모퉁이의 번호 $R$을 인자로 받아서 현재 상황에서 경찰관이 이동해야 할 길모퉁이의 번호를 반환해야 합니다.
함수 start는 nextMove를 호출하기 전 정확히 한 번 호출될 것입니다. start가 $-1$을 반환한다면, nextMove는 호출되지 않습니다. 그렇지 않다면, nextMove 함수는 추적이 끝날 때까지 반복적으로 호출됩니다. 정확히 말해서, 프로그램은 아래 상황 중 적어도 하나가 발생해야만 종료됩니다.
nextMove함수가 경찰관이 이동할 수 없는 길모퉁이의 번호를 반환합니다.- '상황'이 반복됩니다.
- 도둑이 잡힙니다.
예제
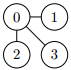
위 그림을 봅시다. 이 경우에는 어떤 길모퉁이도 경찰관에게는 좋은 시작점입니다. 만약 그가 0번 길모퉁이에서 시작한다면, 그는 첫 선택에서 강도를 기다리기만 하면 강도가 알아서 0번 길모퉁이로 올 것입니다. 반면, 경찰관이 다른 길모퉁이에서 시작한다면 그는 강도가 0번 길모퉁이로 들어갈 때까지 기다리다가 들어가는 순간 0번 길모퉁이로 이동하면 됩니다.
이 경우 아래와 같이 함수가 호출될 수 있습니다.
| 함수 호출 | 반환값 |
|---|---|
start(4, [[0, 1, 1, 1], [1, 0, 0, 0], [1, 0, 0, 0], [1, 0, 0, 0]]) |
3 |
nextMove(1) |
3 |
nextMove(0) |
0 |
참고로 start 함수 호출에서 0은 false를, 1은 true를 나타냅니다.
채점
서브태스크 1 (16점)
- $2 \le N \le 500$
- 각 길모퉁이는 정확히 한 개의 골목길과 연결되어 있습니다.
서브태스크 2 (14점)
- $2 \le N \le 500$
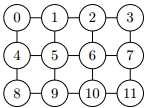
- 길모퉁이들과 골목길은 격자판 모양의 구조를 형성합니다. 격자판은 적어도 2개 이상의 행과 2개 이상의 열을 가지며 번호는 아래 그림과 같이 붙여질 것입니다.
서브태스크 3 (30점)
- $2 \le N \le 100$
서브태스크 4 (40점)
- $2 \le N \le 500$
여러분의 답안은 반드시 두 요구사항을 만족해야 합니다.
- 경찰관이 강도를 잡을 수 있는지 정확히 결정해야 합니다.
- 만약 잡을 수 있다면 경찰을 대신하여 이동하여 성공적으로 도둑을 잡아야 합니다.
서브태스크 1과 2에서 여러분의 답안이 점수를 얻기 위해서는 두 요구사항을 모두 만족해야 합니다. 서브태스크 3과 4에서 첫 번째 요구사항만을 만족하는 답안은 30%의 점수를 얻을 수 있습니다. 만약 여러분의 부분점수를 받고자 한다면, 아무 불가능한 움직임을 반환함으로써 프로그램을 종료하면 됩니다. (nextMove 함수에서 -1을 반환한다거나..)
참고로 평소의 제약조건들 (시간 제한, 메모리 제한, 런타임 에러 없이 프로그램 종료)는 어떤 경우에도 반드시 만족해야 합니다.
실험
coprobber.zip는 표준 입력(stdin)으로부터 데이터를 입력받을 것입니다. 입력의 첫 번째 줄은 길모퉁이의 수 $N$을 포함해야 합니다. 다음 $N$개 줄은 반드시 인접 행렬 $A$를 포함해야 합니다. 각 줄은 $N$개의 수를 포함해야 하며, 수들은 0이나 1 중 하나여야 합니다. 행렬은 반드시 대칭적이어야 하며 주요 대각선의 값은 ($A[i, i]$)은 반드시 0이어야 합니다.
그 다음 줄에는 경찰관이 강도를 잡을 수 있다면 1을, 잡을 수 없다면 0을 포함해야 합니다.
마침내, 만약 경찰관이 강도를 잡을 수 있다면, 도둑의 전략을 나타내는 $N$개의 줄이 주어져야 합니다. 각 줄에는 $0$ 이상 $N-1$ 이하의 정수 $N+1$개를 포함해야 합니다. $r$행의 $c$번째 숫자는 (단 $c < N$), 경찰관이 $r$번 길모퉁이에 있고 강도가 $c$번 길모퉁이에 있을 때 강도가 이동할 길모퉁이의 번호를 나타냅니다. 주요 대각선의 값 ($i$행의 $i$번째 수)은 강도와 경찰관이 같은 곳에 있는 경우이므로 무시됩니다. $r$행의 마지막 수는 경찰의 시작점이 $r$일 때 강도가 출발할 길모퉁이의 번호를 나타냅니다.
아래 입력은 골목길들로 서로 연결된 세 개의 길모퉁이가 있는 도시를 나타냅니다.
3
0 1 1
1 0 1
1 1 0
1
0 2 1 2
2 0 0 2
1 0 0 1
아래 입력은 '예제'에서 주어진 도시와 일치합니다.
4
0 1 1 1
1 0 0 0
1 0 0 0
1 0 0 0
1
0 0 0 0 1
2 0 0 0 2
3 0 0 0 3
1 0 0 0 1
| 파일명 | 크기 |
|---|---|
| coprobber.zip | 6.73 KiB |