통행료 Batch 컴파일 명령

Happyland는 (1부터 $N$까지 번호가 붙여진) N개의 마을과 마을들을 연결하는 (1부터 $M$까지 번호가 붙여진) $M$개의 양방향 도로로 이루어져있다. 1번 마을이 Happyland의 중심마을이다. 마을의 도로망을 이용하여 1번 마을부터 다른 모든 마을들을 방문할 수 있음이 보장되며, 모든 도로는 유료도로이다. 도로 $i$의 통행료는 $c_{i}$센트이며, 도로의 주인에게 납부하여야 한다. 모든 $c_{i}$는 서로 다르다는 것이 알려져 있다. 최근에 $K$개의 도로들이 새로 건설되었으며 소유주는 억만장자인 Mr. Greedy이다. Mr. Greedy는 새 도로들의 통행료를 결정하여 (통행료가 서로 다를 필요는 없다) 내일 발표하여야 한다.

2주 후에 Happyland에서는 대규모 축제가 열릴 예정이다. 많은 참가자들이 중심마을에 모여서 행진을 할 예정이다. 마을 $j$에서는 $p_{j}$명의 참가자들이 중심마을인 1번 마을로 갈 예정이다. 이 사람들은 여행에 필요한 미리 선정된 도로들만을 이용하여 중심마을로 갈 것이며, 그 선정된 도로들은 축제 바로 전날 발표가 될 예정이다. 옛 전통에 따라, 도로 선택은 Happyland에서 가장 부자인 Mr. Greedy가 하게 된다. 또한, 같은 전통에 따라 Mr. Greedy는 선택된 도로의 통행료의 합이 최소가 되도록 도로들을 선택해야 하고, 누구나 마을 $j$에서 마을 1까지의 도로들을 이용할 수 있어야 한다 (그러므로, 통행료가 에지(도로)의 가중치라면 선택된 에지들은 "최소 비용 신장 트리"를 구성하게 된다). 만약 그러한 에지들의 집합이 여러 개가 있다면, Mr. Greedy는 그 중하나를 선택할 수 있다.

Mr. Greedy는 그가 건설한 $K$개의 새로운 도로로부터 얻을 수 있는 수입이 단순히 통행료에만 달려 있지 않다는 것을 잘 알고 있다. 통행료 수입은 그 도로를 여행한 사람들이 지불한 통행료의 합이다. 보다 자세히 말하자면, 만약 $p$명의 사람들이 도로 $i$를 지나간다면, 도로 $i$로부터 얻는 수입은 $c_{i}p$가 된다. 옛날 도로들은 Mr. Greedy의 소유가 아니므로, Mr. Greedy는 새로 건설한 도로로부터만 통행료를 거둘 수 있다.

Mr. Greedy는 엉큼한 계획을 가지고 있다. 그는 도로 선택을 통해 축제기간 동안 거기서 얻는 통행료 수입을 최대화 하려고 한다. 그는 새로운 도로의 통행료를 정하고 (내일 발표해야 하는), 축제 때 그 도로를 선택하여 (축제 하루 전 발표해야 하는), $K$개의 새로운 도로로부터 얻는 수익을 최대화하는 방법을 알기 원한다. 참고로, Mr. Greedy는 전통에 따라 통행료의 합을 최소화하는 도로들을 선택해야만 한다.

여러분은 기자이며 그의 계획을 폭로하기를 원한다. 그렇게 하기 위해, 먼저 Mr. Greedy가 그의 엉큼한 계획을 통하여 얼마의 수입을 얻을 수 있는지를 구하는 프로그램을 작성하여야 한다.

입력 형식

표준입력으로부터 다음의 데이터를 읽는다. 입력의 첫 번째 줄에는 세 정수 $N$, $M$, $K$가 빈칸을 사이에 두고 주어진다. 그 다음 $M$개의 줄에는 초기의 $M$개의 도로들의 정보가 주어진다. $M$개의 줄 중에서 $i$번째 줄에는 세 정수 $a_{i}, b_{i}, c_{i}$가 빈칸을 사이에 두고 주어지는데, 이것은 마을 $a_{i}$와 마을 $b_{i}$ 사이에 양방향 도로가 있고 통행료는 $c_{i}$임을 의미한다. 그 다음 $K$개의 줄에는 새로 건설되는 $K$개의 도로에 대한 정보가 주어진다. $K$개의 줄 중에서 $i$번째 줄에는 두 정수 $x_{i}$, $y_{i}$가 빈칸을 사이에 두고 주어지는데, 이것은 마을 $x_{i}$와 마을 $y_{i}$ 사이에 새로운 양방향 도로가 건설됨을 의미한다. 마지막 줄에는 $N$개의 정수가 하나의 빈칸을 사이에 두고 주어지는데, $j$번째 정수 $p_{j}$는 $j$번 마을로부터 1번 마을로 여행하는 사람의 수를 나타낸다.

입력은 다음의 제약조건을 가진다.

• $1 \le N \le 100,000.$
• $1 \le K \le 20.$
• $1 \le M \le 300,000.$
• $1 \le c_{i}, p_{j} \le 10^{6}$, $i$와 $j$ 각각에 대해.
• $c_{i} \neq c_{i'}$, if $i \neq i'$
• 두 마을 사이에는 (새로 건설되는 도로를 포함하여) 기껏해야 하나의 도로만 존재한다.

출력 형식

출력은 표준출력을 사용한다. 최대 얻을 수 있는 수입을 하나의 정수로 출력한다.

서브태스크

편집자 주: APIO 2013의 규칙을 살펴 보면,

... Hence, during a release-test, if the submission fails at a particular subtask, no further testing will be conducted for subsequent subtasks. ...

즉, 임의의 서브태스크에서 하나의 데이터라도 정확한 답을 내지 못한다면, 이후의 서브태스크는 채점도 하지 않는다는 것입니다. 이 문제에는 이 규칙이 적용되었습니다.

여러분의 프로그램은 다음과 같은 5 가지 조건의 테스트 데이터 세트로 테스트 된다:

1. (16점) $N \le 10$, $M \le 20$, $K = 1$.
2. (18점) $N \le 30$, $M \le 50$, $K \le 10$.
3. (22점) $N \le 1,000$, $M \le 5,000$, $K \le 10$.
4. (22점) $N \le 100,000$, $M \le 300,000$, $K \le 15$.
5. (22점) $N \le 100,000$, $M \le 300,000$, $K \le 20$.

입력과 출력의 예

입력	출력
5 5 1 3 5 2 1 2 3 2 3 5 2 4 4 4 3 6 1 3 10 20 30 40 50	400

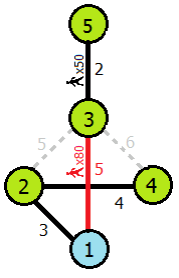
이 예제에서는, Mr. Greedy는 새로운 도로 (1,3)의 통행료를 5센트로 하여야 한다. 이것으로, 그는 통행료가 14 센트로 최소가 되는 도로들 (3,5), (1,2), (2,4) 그리고 (1,3)을 선택할 수 있다. 3번 마을로부터 30명, 5번 마을로부터 50명이 1번 마을로 가기 위해 새로운 도로를 지날 것이기 때문에 $(30 + 50) \times 5 = 400$ 센트의 수입을 얻을 수 있다.

한편, 만약 새로운 도로 (1,3)의 통행료를 10센트로 한다면, 전통에 따라 Mr. Greedy는 통행료의 합이 최소가 되는 (3,5), (1,2), (2,4) 그리고 (2,3) 도로를 선택해야 한다. 그러므로, 축제기간 동안 새 도로 (1,3)으로부터는 아무런 수입을 얻을 수 없다.